 |
|
 |
|
平面図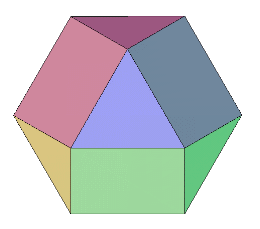 |
側面図 |
|---|---|
立面図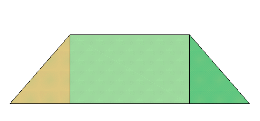 |
俯瞰図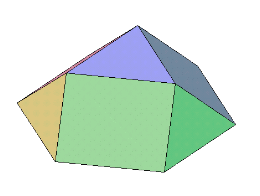 |
 |
(参考)マウスでドラッグして下さい。 |
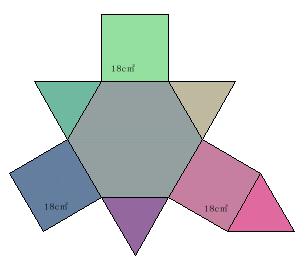
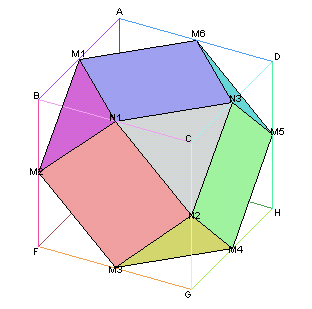
左図では、立方体の辺AB、BF、FG、GH、HD、DAの各中点をM1、M2、M3、M4、M5、M6、および辺BC、CG、CDの各中点をN1、N2、N3とする。
M1、M2、M3、M4、M5、M6を結んで出来る図形は正六角形。
N1、N2、N3を結んで出来る図形等は正三角形。
M1、N1、N3、M6を結んで出来る図形等は正方形。
となり、左図は問題の立体と同じものであることが分かる。
さて、正六角形を含む平面で、立方体はちょうど二分割されており、求める立体はさらに、M1.B.M2.N1等4つの三角錐をのぞいたものである。
まず、立方体の一辺の長さを求めよう。
直角三角形A.M1.M6の面積は正方形M1.N1.N3.M6の4分の1、従ってそれを二つ合わせた正方形の面積は半分の18/2=9cm2。
よって、直角三角形の一辺の長さは3cm、立方体の一辺の長さは6cmとなる。さて、立方体の体積は、6*6*6=216cm3。
三角錐の体積は、1/3*(1/2*3*3)*3=9/2cm3。従って、求める体積は、216/2−9/2*4=108−18=90cm3となる。