第１０４問の解答

---

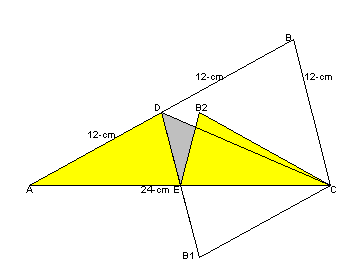
１．問題　［平面図形］

左図のような、ＡＢ＝ＡＣ＝２４cm、ＢＣ＝１２cmの二等辺三角形ＡＢＣがあります。また、ＡＢの真ん中の点をＤとします。 　この三角形を、ＤＣを折り目として折り返し、さらにＥＣを折り目として折り返します。また、このときＢが移動した点をそれぞれＢ1、Ｂ2とします。 　では、ＤＢ2は何cmでしょうか。

---

２．解答例１

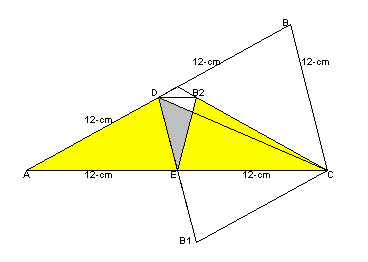左図のように、ＥをＡＣの中点として、ＤＥの延長線上にＥＢ1＝６ｃｍとなるようにＢ1をとる。この点が実はＢを折り返した点になることを示す。

中点連結定理により、ＤＥとＢＣは平行、ＤＥ＝ＢＣ/２＝６ｃｍ。従って、ＤＢ１＝ＤＥ＋ＥＢ１＝１２ｃｍ。
すると、ＤＢ１とＢＣが平行かつＤＢ１＝ＢＣ＝１２ｃｍとなるので、ＤＢ１ＣＢは平行四辺形。
よって、Ｂ１Ｃ＝ＤＢ＝１２ｃｍとなる。
これは、Ｂ１がＤＣを折り目にＢを折り返した点に他ならないことを意味する。

すると、ＥＢ２＝ＥＢ１＝６ｃｍ、Ｂ２Ｃ＝Ｂ１Ｃ＝１２ｃｍとなることが分かる。
すなわち、△ＡＤＥ、△ＣＢ２Ｅ、△ＣＢ１Ｅは全て合同で、かつ△ＡＢＣに相似である（相似比１：２）。

これから、∠ＣＥＢ２＝∠ＡＥＤ＝∠ＡＤＥとなり、∠ＤＥＢ２＝１８０度−（∠ＡＥＤ＋∠ＡＤＥ）＝∠ＤＡＢ。
すなわち、△ＤＥＢ２は二等辺三角形で頂点の角が△ＡＤＥの頂点の角と等しいので、△ＡＤＥと相似である。

すると、ＤＥ＝ＥＢ２＝６ｃｍであるから相似比は１：２。よって、ＤＢ２＝ＤＥ／２＝３ｃｍとなる。

以上

---

３．解答例２

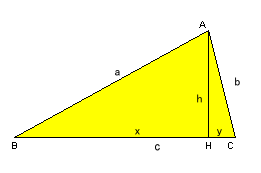
私自身が最初に解いたときは、解答例１の最後の△ＤＥＢ２が△ＡＤＥあるいは△ＡＢＣと相似であることに気が付かなかったので、次の補題を用いた。

補題：△ＡＢＣでＨはＡからＢＣに引いた垂線の足とする。
　　ｘ＝（ｃ^２＋ａ^２−ｂ^２）／２ｃ、ｙ＝（ｃ^２−ａ^２＋ｂ^２）／２ｃ

証明：
　ｘ^２＋ｈ^２＝ａ^２、ｙ^２＋ｈ^２＝ｂ^２より、　ｘ^２−ｙ^２＝ａ^２−ｂ^２
（ｘ−ｙ）（ｘ＋ｙ）＝ａ^２−ｂ^２
しかるに、ｘ＋ｙ＝ｃより、ｘ−ｙ＝（ａ^２−ｂ^２）／ｃ
これから、ｘ、ｙを求めると補題のようになる。

さて、ＤＢ２とＡＣは平行より、ＤＢ２の長さは、補題を△ＤＡＥの場合に適用したｙの２倍。
すなわち、ＤＢ２＝２＊（１２^２−１２^２＋６^２）／（２＊１２）＝６^２／１２＝３ｃｍ。

以上

---