戞侾侽俆栤偺夝摎
侾丏栤戣丂乵暯柺恾宍乶
 |
|
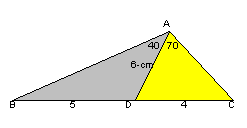
俀丏夝摎椺侾乮倠倳倰倝丄俆俇俁旵栚偺僫僉僂僒僊偝傫乯
捀揰俠偐傜捈慄傪曈俢俙偵暯峴偲側傞傛偆偵堷偒丄曈俛俙偺墑挿慄偲偺岎揰傪俤偲偡傞丅
佢俠俙俤亖侾俉侽亱亅乮佢俛俙俢亄佢俢俙俠乯亖侾俉侽亱亅乮係侽亱亄俈侽亱乯亖俈侽亱丅
俙俢偲俤俠偼暯峴偩偐傜丄佢俙俤俠亖佢俛俙俢亖係侽亱丄佢俙俠俤亖佢俢俙俠亖俈侽亱丅
廬偭偰丄嚈俙俤俠偼擇摍曈嶰妏宍偲側傝丄俤俙亖俤俠丅
偝偰丄嚈俙俛俢偲嚈俤俛俠偼憡帡偱丄憡帡斾偼俛俢丗俛俠亖俆丗俋
傛偭偰丄俤俠亖俙俢仏俋乛俆亖俇仏俋乛俆亖俆係乛俆丅
廬偭偰丄俤俙亖俤俠亖俆係乛俆丅
傛偭偰丄俙俛亖俤俙仏俆乛係亖乮俆係乛俆乯仏乮俆乛係乯亖俀俈乛俀丅
埲忋
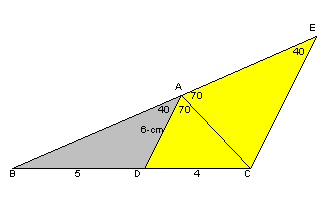
俁丏夝摎椺俀乮媑愳偝傫丄偄偍傫偲傜傫傉偝傫乯
俛俙偺墑挿慄忋偵揰俥傪俙俥亖俇們倣偲側傞傛偆偵偲傞丅
夝摎椺侾偲摨條偵偟偰丄佢俥俙俠亖俈侽亱丅
屘偵仮俥俙俠偼仮俢俙俠偲崌摨偲側傝丄柺愊傕摍偟偄丅
偝偰丄俛俢丗俢俙亖俆丗係傛傝丄仮俙俛俢偺柺愊丗仮俙俢俠偺柺愊亖俆丗係丅
傛偭偰丄仮俠俛俙偺柺愊丗仮俠俥俙偺柺愊亖俋丗係丅
傛偭偰丄俛俙丗俙俥亖俋丗係偲側傝丄俛俙亖俙俥仏俋乛係亖俇仏俋乛係亖俀俈乛俀丅
埲忋
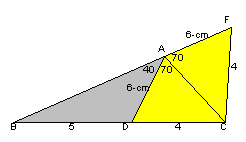
係丏夝摎椺俁乮H.Takai偝傫丄惔愳堢抝偝傫乯
俢傪偲偍傝俛俙偵暯峴偵捈慄傪堷偒俙俠偲偺岎揰傪俧偲偡傞丅
佢俙俢俧亖佢俛俙俢亖係侽亱丄傛偭偰佢俙俧俛亖俈侽亱丅
偡側傢偪丄仮俢俙俧偼擇摍曈嶰妏宍偲側傝丄俢俧亖俢俙亖俇們倣丅
偝偰丄仮俠俢俧偲仮俠俛俙偼憡帡偱偁傝丄憡帡斾偼俠俢丗俠俛亖係丗俋丅
傛偭偰丄俙俛亖俢俧仏俋乛係亖俇仏俋乛係亖俀俈乛俀丅
埲忋
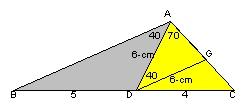
係丏夝摎椺係乮倠倳倰倝乯

仮俙俛俠偺柺愊傪俽偲偡傞丅
仮俙俛俢丗仮俙俢俠亖俛俢丗俛俠亖俆丗係丅
傛偭偰丄仮俙俢俠偺柺愊亖俽仏係乛俋丅
偝偰丄仮俠俢俧偲仮俠俛俙偼憡帡偱偁傝丄憡帡斾偼俠俢丗俠俛亖係丗俋丅
俽丂丂丂丂丂亖侾乛俀仏俙俛仏俙俠仏倱倝値乮侾侾侽亱乯丂丒丒丒丂乮侾乯
俽仏係乛俋亖侾乛俀仏俙俠仏俙俢仏倱倝値乮俈侽亱乯丂丂丒丒丒丂乮俀乯
乮侾乯偲乮俀乯偺椉曈傪偦傟偧傟妱傞偲丄
俋乛係亖俙俛乛俙俢仏倱倝値乮侾侾侽亱乯乛倱倝値乮俈侽亱乯
偲偙傠偑丄俙俢亖俇們倣丄倱倝値乮侾侾侽亱乯亖倱倝値乮俈侽亱乯偩偐傜
俙俛亖俇仏俋乛係亖俀俈乛俀丅
埲忋
丂