第１０６問の解答

１．問題　［速さ］

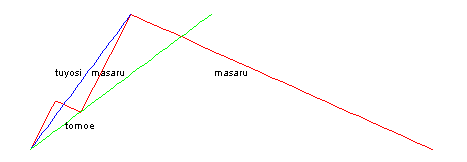
　マサル君、トモエさん、ツヨシ君の３人が、上りのエスカレーターに同時に乗りました。

　トモエさんはじっとしていましたが、マサル君とツヨシ君はエスカレーター上で歩きました。
　何段か上ったところで、マサル君は下り始め、トモエさんのところまでくるとまた上り始めました。
　すると、その後１２段歩いたところでツヨシ君と同時に上の階に着いたそうです。

　また、マサル君がこの上りエスカレーターを上の階から歩いて下りると、７２段歩いたところで下の階に着くそうです。

　マサル君は、ツヨシ君の２倍の速さで上り下りできます。

　では、この上りエスカレーターは全部で何段あったでしょうか。

２．解答例

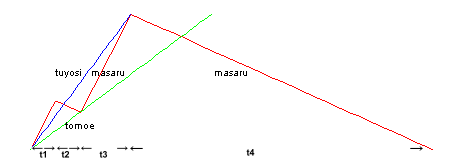
マサル君が引き返すまでの時間をｔ１、そこからトモエさんに出会うまでの時間をｔ２、そこから上の階に着くまでの時間をｔ３、そして下りに要する時間をｔ４とする。

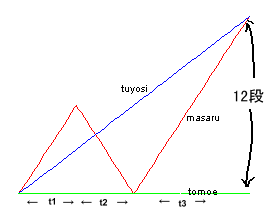
エスカレータが静止した状態で考えると、マサル君がエスカレータをｔ１だけ上がって、ｔ２だけ下りて元へ戻ることとなるので、ｔ１＝ｔ２。
また、つよし君が（ｔ１＋ｔ２）＋ｔ３で上った分をマサル君は倍の速さでｔ３で上がったのだから、ｔ１＋ｔ２＝ｔ３となる。
従って、ｔ１：ｔ２：ｔ３＝１：１：２となる。

さて、ｔ１を単位時間として考える。
マサル君がエスカレータを上り下りする速さは、単位時間あたり１２／２＝６段となる。

すると、ｔ４で７２段下りたのだから　ｔ４＝７２／６＝１２。

さて、求めるエスカレータの段数をｄ、マサル君が上りに要した４単位時間にエスカレータ自身が動いた段数をＶとすると、
　　　　　　　Ｖ＋１２＝ｄ、３Ｖ−７２＝−ｄ
これより、Ｖ＝１５、ｄ＝２７を得る。

よって、求めるエスカレータの段数は２７段である。

以上