第１０７問の解答

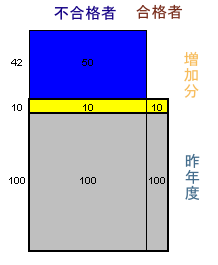
１．問題　［割合］

ある中学校の本年度の入試は、受験者数は５２％、合格者数は１０％、不合格者数は６０％、昨年度よりも増えました。

また、本年度の合格者の平均点は合格基準点よりも２４点高く、不合格者の平均点は合格基準点よりも１４点低かったそうです。

また、全受験者の平均点は２１６.４点でした。

では、本年度、この中学校の合格基準点は何点だったでしょうか。

２．解答例１

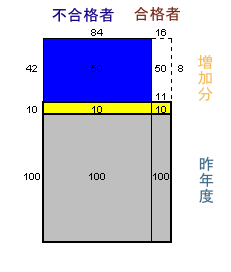
昨年度の合格者、不合格者：

不合格者の増加分６０％のうち、合格者の増加分と同じ１０％（黄色部分）を除いた５０％（青色部分）について考える。

昨年度の受験者数を１００（灰色部分）とすると、受験者全体の増加分５２から１０（黄色部分）を除いた４２となる。

従って、合格者が仮に不合格者と同じ６０％増加したとしたら、今より５０−４２＝８だけ多くなる（白色部分）。

昨年度の不合格者数と合格者数の比は、この青色部分と白色部分の比４２：８＝８４：１６となる。

本年度の合格者、不合格者：

次に、本年度の不合格者数を８４とすると、６０％増加したときの合格者数は１６である。実際には、１０％しか増加しなかったのだから１６＊（１１０／１６０）＝１１となる。

すなわち、今年度の不合格者数と合格者数の比は、８４：１１となる。

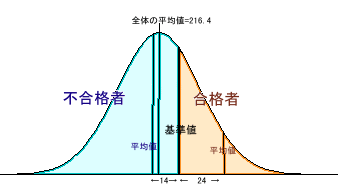
全体の平均値、基準値：

不合格者の平均値を仮に０とすると、合格者の平均値は１４＋２４＝３８点となる。

すると、全体の平均値＝(0*84+38*11)/(84+11)
　　　　　　　　　　＝19*2*11/19*5＝４.４点となる。

実際の平均値は２１６.４点だから、
不合格者の平均値＝２１６.４−４.４＝２１２点。
従って、基準値＝２１２＋１４＝２２６点と分かる。

以上

３．解答例２

x0:昨年度の合格者数、y0:不合格者数、z0:受験者数
x1:本年度の合格者数、y1:不合格者数、z1:受験者数、p:基準値　とおく。

題意より、
(1)  z0 = x0 + y0
(2)  z1 = x1 + y1
(3)  x1 = 11/10 x0
(4)  y1 = 16/10 y0
(5)  z1 = 152/100 z0
    (p + 24) x1 + (p - 14) y1
(6) ------------------------- = 2164/10
               z1

(2)、(3)、(4)より、
  (7) 152/100 z0 = 11/10 x0 + 16/10 y0

(1)*16/10-(7)より、
  (8)  2/25 z0 = 1/2 x0  ∴ x0 =  4/25 z0

(7)-(1)*11/10より、
  (9) 21/50 z0 = 1/2 y0  ∴ y0 = 21/25 z0

(3)、(4)より、
 (10)    x1 = 22/125 z0、 y1 = 168/125 z0

	(6)、(10)、(5)より、
	  (p + 24) 22/125 z0 + (p - 14) 168/125 z0
	 ------------------------------------------ = 2164/10
	               152/100 z0

	よって、
	  p-48/5 = 1082/5   ∴ p = 226

以上