第１０８問の解答

１．問題　［平面図形］

　左図のように、一辺１２cmの正方形ＡＢＣＤの上に、面積の違う正方形ＥＦＧＨを重ねました。

　すると、正方形ＥＦＧＨの各辺の中点（Ｐ、Ｑ、Ｒ、Ｓ）は、正方形ＡＢＣＤの各辺を１：２に分ける点に 重なりました。

　このとき、正方形ＥＦＧＨの面積を求めなさい。

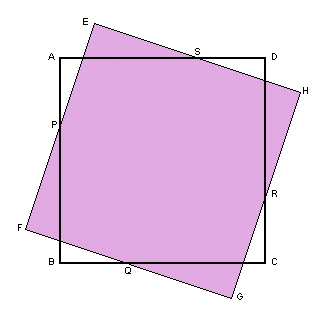
２．解答例１（ほそたにさん、H.Takaiさん、柚奇　神太郎さんほか）

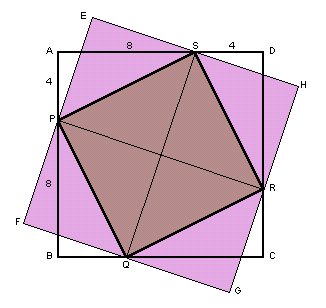
△ＡＰＳの面積：

ＡＰ＝ＡＢ／３、ＡＳ＝ＡＤ＊２／３より、
△ＡＰＳ＝ＡＰ＊ＡＳ／２＝ＡＢ＊ＡＤ／９＝□ＡＢＣＤ／９。

ＰＱＲＳの面積：

四辺形ＰＱＲＳは、明らかに正方形であり、
□ＰＱＲＳ＝□ＡＢＣＤ−４＊ △ＡＰＳ
　　　　　＝ ５＊△ＡＰＳ＝５／９＊□ＡＢＣＤ
　　　　　＝５／９＊１４４＝８０ｃｍ２。

□ＥＦＧＨの面積：

Ｐ、Ｑ、Ｒ、Ｓが□ＥＦＧＨの各辺の中点であることから、□ＰＱＲＳ＝□ＥＦＧＨ＊２。

よって、 □ＥＦＧＨ＝□ＰＱＲＳ＊２＝１６０ｃｍ２。

以上

３．解答例２（ありさのお父さん、わかさひ君、ｋｕｒｉ）

△ＡＰＳは直角三角形であり、ＡＰ＝４，ＡＳ＝８から、 ＰＳ２＝ＡＰ２＋ＡＳ２＝８０。
よって、 □ＥＦＧＨ＝８０ｃｍ２。

従って、□ＥＦＧＨ＝□ＰＱＲＳ＊２＝１６０ｃｍ２。

以上