第109問の解答
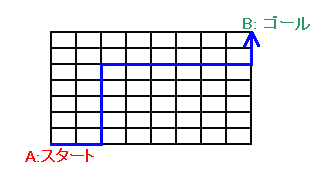
1.問題 [場合の数]
|
|
2.解答例1(図解的解法:H.Takaiさん、ぐっちさんほか)
|
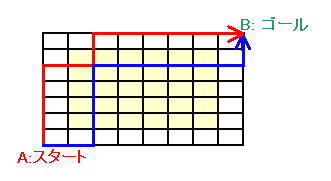
2度目の曲がり角は、格子の内側(左図の黄色部分)でなければならないことは容易に分かる。 また、1度目と3度目の曲がり角は、2度目の曲がり角の下端・右端(青色の場合)か左端・上端(赤色の場合)の2通りしかない。 よって、 求めるルートの数は、格子の内側の点の数×2=7×6×2 =84通りとなる。 |
以上
3.解答例2(順列組み合わせ的解法:KINさん、563匹目のナキウサギさん、kuri)
|
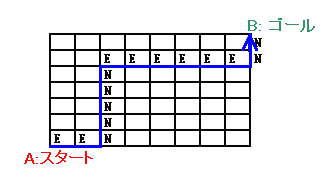
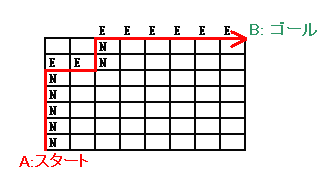
経路を右方向に進むとをE、上方向へ進むことをNで表すことにする。 3回曲がるということは、ENEN(青色の場合)、NENE(赤色の場合)の進み方の2通りということになる。 ところで、どちらの場合もEの個数は合計8個であり、初めの個数(1〜7)が決まれば後の個数は自動的に決まる。従って、それぞれEの並び方は7通り。 同様にして、Nの並び方は、それぞれ(7−1)=6通り。 よって、求めるルートの数は、7×6×2=84通りとなる。 |
以上