戞侾侾侽栤偺夝摎
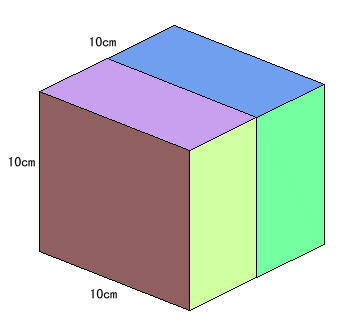
侾丏栤戣丂乵惍悢偺惈幙乶
|
|
俀丏夝摎椺
|
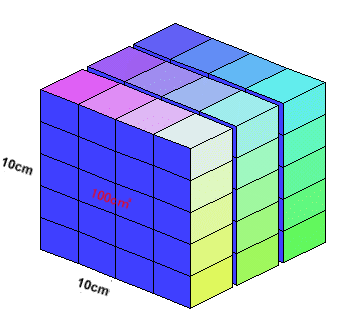
丂俁曽岦偵暘妱偡傞悢傪倶丆倷丆倸屄偲偟丄x亝y亝z偲壖掕偡傞丅偙偺偲偒丄愗傞夞悢偼丄崌寁(x-1)+(y-1)+(z-1)=(x+y+z-3)夞偱偁傞丅 丂暘妱偝傟傞棫曽懱偼俇侽屄偩偐傜丄x*y*倸=60偱偁傝丄60=22亊3亊5偲慺場悢暘夝偱偒傞丅 丂傑偨丄尦偺棫曽懱偺傂偲偮偺柺偺柺愊傪俽偲偡傟偽丄暘妱偝傟偨棫曽懱偺昞柺愊S'偼丄俁曽岦偵暘偗偰悢偊傞偲丄偦傟偧傟俽偺2*x攞丄2*y攞丄2*z攞偲側傞偺偱丄S'亖2*(x+y+z)*S 偲側傞丅 丂傛偭偰丄暘妱偝傟偨棫曽懱偺昞柺愊傪嵟彫偵偡傞偙偲偼丄x+y+z傪嵟彫偵偡傞偙偲偲側傝丄偦偺偨傔偵偼x丄y丄z偺愊偑堦掕側偺偱丄弌棃傞尷傝x丄y丄z偺抣傪嬤偔偡傞昁梫偑偁傞丅 丂廬偭偰丄x=3丄y=4丄z=5偺偲偒偑嵟彫偱偁傝丄愗傞夞悢偼(3+4+5-3)亖俋夞丄昞柺愊S'亖2*12*100亖俀係侽侽們噓偲側傞丅 |
乮嶲峫乯
丂x丄y丄z偑惓偺幚悢偺偲偒偵偼丄憡壛暯嬒亞憡忔暯嬒傛傝丄
x+y+z亞3*3併x*y*z亖3*3併俇侽亖11.74乮摍崋偼丄x亖y亖z亖3併俇侽亖3.91偺偲偒丅乯
廬偭偰丄x丄y丄z偑惍悢偺偲偒丄x+y+z亞侾俀偲側傞丅丂傕偪傠傫丄x丄y丄z偼惍悢偱偁傞偺偱丄偲傝偆傞抣偺慻傒崌傢偣偐傜嵟彫抣傪媮傔傞偺偑僆乕僜僪僢僋僗偲巚傢傟傞偑丄斚嶨偵側傞偺偱愢柧偼徣棯偡傞偙偲偲偟偨丅
丂側偍丄x丄y丄z偑侾偱偼側偄丄偡側傢偪奺曽岦偲傕昁偢堦夞埲忋愗傞偲偄偆壖掕偑偁傟偽丄慻傒崌傢偣偺悢偼偐側傝彮側偔側傝丄x=2丄y=3丄z=10(x+y+z亖15)丄x=2丄y=5丄z=6(x+y+z亖13)丄x=3丄y=4丄z=5(x+y+z亖12)偺俁偲偍傝偱偁傞丅
埲忋