第１１１問の解答

１．問題　［平面図形］

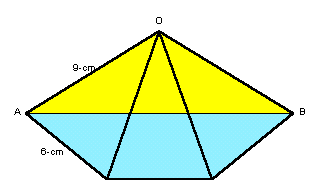
　左図のような底辺の長さが６cm、等しい２辺の長さが９ｃｍの二等辺三角形を３つ並べたとき、ＡＢの長さはいくらか？

２．解答例１

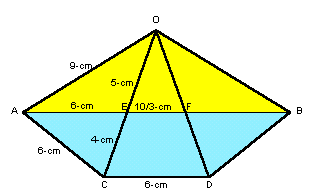
　左図のように、各点に名前を付ける。

　△ＯＥＦは△ＯＣＤに相似な二等辺三角形だから、∠ＯＥＦ＝∠ＯＣＤ＝∠ＡＣＥ。

　また、対頂角ゆえ、∠ＯＥＦ＝∠ＡＥＣ。よって、∠ＡＣＥ＝∠ＡＥＣとなり、△ＡＥＣも△ＯＣＤに相似な三角形となる。

　従って、ＡＥ＝ＡＣ＝６ｃｍ、ＣＥ＝ＡＣ＊６／９＝４ｃｍとなる。

　よって、ＯＥ＝ＯＣ−ＣＥ＝９−４＝５ｃｍ。△ＯＥＦは△ＯＣＤに相似だったから、ＥＦ＝ＯＥ＊６／６＝５＊６／９＝１０／３ｃｍとなる。

故に、ＡＢ＝ＡＥ＋ＥＦ＋ＦＢ＝６＋１０／３＋６＝４６／３ｃｍとなる。

以上

３．解答例２

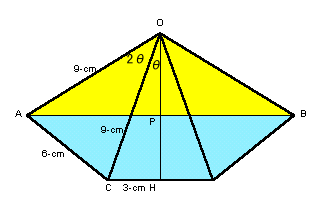θ＝∠ＣＯＨ＝∠ＣＯＤ／２とする。ｓｉｎθ＝ＣＨ／ＯＣ＝３／９。よって、θ＝ｓｉｎ-1(１/3)。

∠ＡＯＨ＝∠ＡＯＣ＋∠ＣＯＨ＝３θ。故に、ＡＰ＝ＯＡ＊ｓｉｎ∠ＡＯＨ＝９＊ｓｉｎ３θ。

しかるに、ｓｉｎ３θ＝３ｓｉｎθ−４ｓｉｎ３θ＝３＊１／３−４＊（１／３）３＝２３／２７。

よって、ＡＰ＝９＊２３／２７＝２３／３ｃｍ。ＡＢ＝２＊ＡＰ＝４６／３ｃｍ。