第112問の解答
1.問題 [差集め算]
|
マサル王国、アーキ王国、トーラ王国の通貨は、コインのみでそれぞれ1種類しかなく、サール、アーキ、トーラといいます。 ある品物Aを、それぞれの国で買ったら、アーキの枚数はサールより7枚多く、トーラはアーキよりさらに21枚多く必要です。 また、同じ枚数の硬貨でイモを買ったとき、アーキではサールより4個少なく、トーラではアーキより8個少ないイモしか買えません。 さて、 2)72アーキする品物Bは何サールでしょうか。 |
2.解答例(武田浩紀さん他)
|
各通貨の貨幣価値の比をr1:r2:r3とする。 (1サール=r1円、1アーキ=r2円、1トーラ=r3円) 品物Aの価格をxサールとすると、(x+7)アーキ、(x+28)トーラとなる。 また、用意した枚数のサールで買えるイモの個数をy個とすると、アーキでは(y−4)個、トーラでは(y−12)個買えることとなる。 従って、xy=(x+7)(y−4)=(x+28)(y−12)となる。 (方程式で解く)上記式より、−4x+7y=28、−3x+7y=84を得るので、これを解いてx=56サール、y=36個を得る。 すると、貨幣価値の比は、36:32:24となるので、72アーキする品物Bは、72×32/36=64サールとなる。 (面積図で解く)上記式を図示すると、下図のようになる。A、B、・・、Fはそれぞれの長方形の面積とする。 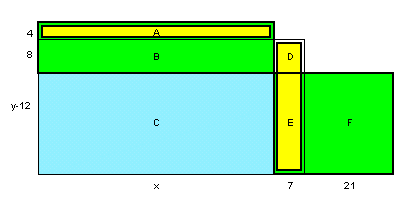 A+B+C=B+C+D+Eより、A=D+E(黄色の部分)。 よって、A=1とすると、B=2。E+F=A+B=3より、E=3/4。 したがって、x:7=B:D=2:1/4=8:1。よって、x=8×7=56。 B:C=D:E=1/4:3/4=1:3。C=B×3=6。よって、y=(A+B+C)×4=36。 以下、同上。 |
以上