第113問の解答
1.問題 [平面図形]
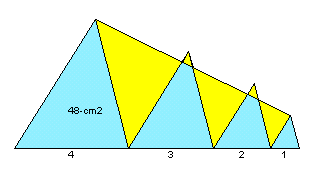
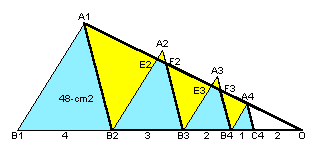
|
|
2.解答例1(H.Takaiさん、パリンさん他)
下図のとおり、A1.A4の延長線とB1.C4の延長線の交点をOとする。
参考図1
(C4.Oの長さ)
△A1.B2.Oと△A4.B4.Oは、相似で、相似比はA1.B2:A4.C4=4:1。
よって、B2.C4:C4.O=3:1。C4.O=6×1/3=2。(△A1.B2.Oの面積)
△A1.B2.Oは、△A1.B1.B2と高さが同じで、底辺の比が4:8。
従って、△A1.B2.O=△A1.B1.B2×2=96cm2(辺の長さ)
先ほど同様に、上図太線の各三角形は相似だから、
A1.F2:F2.F3:F3.A4:A4.O=3:2:1:2。参考図2
また、上図より、同様に三角形の相似から、
従って、A4.O=3とすると、F3.A4=1.5。
A1.E2:E2.E3:E3.A4:A4.O=4:3:2:3。
E3.F3=E3.A4−F3.A4=2−1.5=0.5。
F2.F3=A4.O=3、F2.E3=F2.F3−E3.F3=3−0.5=2.5。
E2.F2=A4.O=3、E2.F2=E2.E3−F2.E3=3−2.5=0.5。
A1.F2=A4.O×3/2=4.5、A1.E2=F2.E3−E2.F2=4.5−0.5=4。
辺の長さの比は、4:0.5:2.5:0.5:1.5=8:1:5:1:3。(黄色の三角形の面積)
黄色の三角形は、互いに相似だから、面積比は辺の比の2乗に比例する。
すなわち、64:1:25:1:9である。ところで、やはり三角形の相似より、四角形A1.B1.B2.E2の面積=△A1.B1.O×B1.B2/B1.O=(48+96)×4/12=32cm2。
よって、黄色の三角形の面積は、それぞれ32、0.5、12.5、0.5、4.5cm2となり、合計=32+0.5+12.5+0.5+4.5=50cm2。
以上
3.解答例2(kuri他)
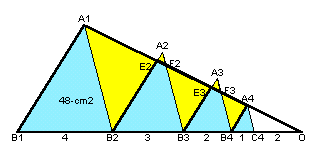
△A1.B2.O=△A1.B1.B2×2=96cm2までは、解答例1に同じ。
参考図1
上記参考図1より、
△A1.B2.O、△F2.B3.O、△F3.B4.O、△A4.C4.Oはそれぞれ相似で、相似比は、8:5:3:2。 よって、面積比は、64:25:9:4となり、面積は、96cm2、37.5cm2、13.5cm2、6cm2となる。参考図2
上記参考図2より、
従って、
△A1.B1.O、△E2.B2.O、△E3.B3.O、△A4.B4.Oはそれぞれ相似で、相似比は、12:8:5:3。 よって、面積比は、144:64:25:9となり、面積は、144cm2、64cm2、25cm2、9cm2となる。
△A1.B2.E2=△A1.B2.O−△E2.B2.O=96−64=32cm2、
△F2.B3.E3=△F2.B3.O−△E3.B3.O=37.5−25=12.5cm2、
△F3.B4.A4=△F3.B4.O−△A4.B4.O=13.5−9=4.5cm2。
また、四角形E2.B2.B3.F2=△E2.B2.O−△F2.B3.O=64−37.5=26.5cm2。
同様に、四角形E3.B3.B4.F3=△E3.B3.O−△F3.B4.O=25−13.5=11.5cm2。ところが、△A1.B1.B2、△A2.B2.B3、△A3.B3.B4は相似で、相似比は4:3:2。
よって、面積比は16:9:4、面積は48cm2、27cm2、12cm2となる。従って、A2.E2.F2=△A2.B2.B3−E2.B2.B3.F2=27−26.5=0.5cm2、
A3.E3.F3=△A3.B3.B4−E3.B3.B4.F3=12−11.5=0.5cm2となる。以上から、求める黄色い三角形の面積の和は、32+0.5+12.5+0.5+4.5=50cm2となる。
以上