第114問の解答
1.問題 [速さ]
|
16人のメンバーが、A地点から30km離れたT地点に行くことになりました。 ところが16人には、4人乗りの乗用車が1台あるだけです。そこで、1人が運転手となって、残りの15人を3人ずつ順番に乗せて運ぶことになりました。 まず、3人(運転手を入れると4人)を乗せた車がA地点を出発します。同時に、残りの12人は歩いてT地点に向かって出発します。車はT地点に着く手前d1kmの地点で3人を降ろし、A地点方面に引き返します。降りた3人はT地点に向かって歩き始めます。 次に、引き返してきた車は、途中まで歩いてきた12人に出会うと、その中の3人を乗せて再びT地点に向かいます。もちろん、残りの9人はそのまま歩いてT地点に向かいます。車は、先に歩いている3人に追いつくと、その地点で乗っていた3人を降ろし、またまたA地点方面に引き返します。降りた3人は、歩いてきた3人と一緒にT地点に向かいます。 これを繰り返したところ、最後の3人を乗せた車が歩いている12人に追いついた地点がちょうど目的地のT地点であったそうです。 乗用車の速さは毎時60km、歩く速さは毎時4kmです。 (1) d1は、 何kmでしょうか?(2) 乗用車は合計で 何km走ったでしょう? |
2.解答例1(長野美光さん、TORAさん、柚本神大朗さん他)
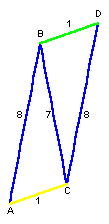
左図のように、出発点をA、最初の3人を下ろす地点をB、歩き組と再び出会う地点をC、2度目に3人を下ろす地点をDとする。
歩き組と自動車の速度比は、4:15=1:15なので、歩き組がAからBまで進む距離を1とすると、3人を乗せた歩き組は、その間15進む。
このとき、往きは8、帰りは7だけ進むこととなる。同様に、最初に下りた3人がBから1だけ進む間に、自動車は15だけ進むので、結局CからDまで自動車が進む距離は、AからBと同じ8である。
すなわち、ABCDは、平行四辺形となる。
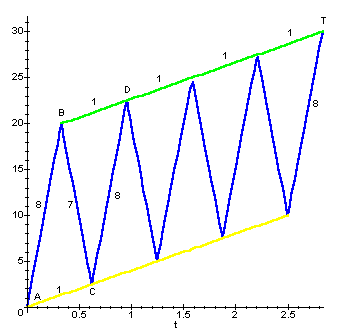
結局、左図のように自動車の進む経路が青色の線、歩き組の進む経路は、最初が黄色、下りた後が緑色の線となる。
従って、最初の3人は、8だけ自動車で進んだあと4だけ歩き、T地点へ到着することとなる。
すなわち、A地点からT地点の距離は30kmなので、自動車に乗った距離は、30×8/12=20Km、歩く距離は、30×4/12=10Kmとなる。
そして、自動車が進んだ距離の合計は、15×4+8=68だけなので、10km/4×68=170kmとなる。
以上