第１１６問の解答

１．問題　［平面図形］

問題図

　左図は、平行四辺形ＡＢＣＤの頂点Ｂと、辺ＤＣを２：３の比に分ける点Ｐを結び、さらに頂点ＡからＢＰに垂線ＡＨを下ろしたところを表しています。

　このとき、ＡＤ＝ＡＨ＝ＨＢ＝ＢＣ＝３cmとなりました。

　では、平行四辺形ＡＢＣＤの面積は何cm2でしょうか。

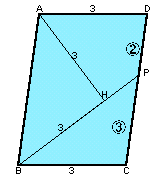
２．解答例（長野　美光さん、ありさのお父さん、ＴＯＲＡさん、kuri他）

ＡＤとＢＰを延長して交わる点をＱとする。

参考図


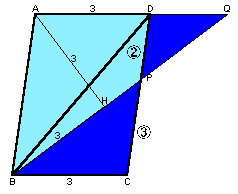
すると、△ＤＱＰと△ＣＢＰは相似となり、相似比はＤＰ：ＣＰ＝２：３、 従って、ＤＱ＝ＣＢ×２／３＝３×２／３＝３ｃｍとなる。

　次に、△ＡＨＱを見てみると、斜辺ＡＱ＝ＡＤ＋ＤＱ＝５ｃｍ、ＡＨ＝３ｃｍの直角三角形である。よって、ＱＨ＝４ｃｍと分かる。

　さて、△ＡＢＱの面積＝１／２×ＢＱ×ＡＨ＝１／２×（３＋４）×３＝２１／２ｃｍ2。

△ＡＢＤと△ＡＢＱは、高さが共通だから、面積比は底辺の比に等しい。
従って、△ＡＢＤの面積＝△ＡＢＱの面積×３／５＝２１／２×３／５＝６．３ｃｍ2。

よって、平方四辺形ＡＢＣＤの面積＝△ＡＢＱの面積×２＝１２．６ｃｍ2となる。

以上