第117問の解答
1.問題 [規則性]
|
円のまわりに、1〜200までの番号の書かれたボールを右周りに小さい順に並べていきます。 このボールを1のボールから右周りに1つおきに取っていきます。円を一周してしまった後もボールがなくなるまでこの作業を続けます。 このとき、最後に取ることになるボールは何番のボールでしょうか。 |
2.解答例1(H.Takaiさん、Hiroさん、kuri他)
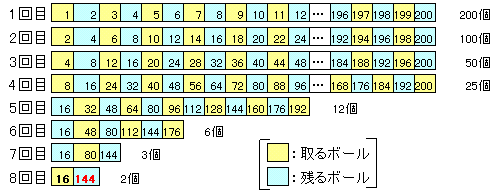
まず、1回目に、奇数を全て取ることになり、偶数が残ります。
次に、2回目は、4の倍数が残り、それ以外を取ることになります。
また、3回目は、8の倍数が残り、それ以外を取ることになります。
そして、4回目は、16の倍数が残り、それ以外を取ることになります。ところが、4回目で残ったボールは、25個で奇数になりますので、5回目は2個目の32から取っていくことになるので、32の倍数を除き、それ以外が残ることとなります。
以下、図のごとく取っていき、最後に144が残ります。以上
2.解答例2(TORAさん、kuri他)
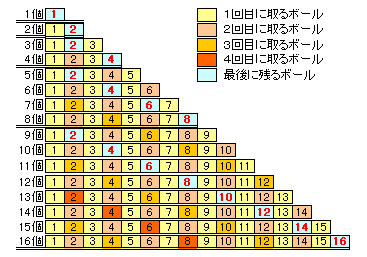
1個から、16個までの場合を考えてみます。
すると、次のような規則性があることが分かります。
すなわち、2のべき乗単位で周期的に、2,4,6,8・・・・と2づつ増えていくようです。
従って、200個の場合、これより小さな2のべき乗は128ですから、最後に残るのは、(200−128)×2=144となることが分かります。
以上
3.解答例3(ありさのお父さん、kuri他)
解答例2で予想した規則性を式にしてみましょう。
ボールの個数がn個のとき、最後に残る番号をf(n)とします。まず、f(1)=1、f(2)=2は明らかですね。
ちなみに、nが2のべき乗に等しいとき、m=n/2だから、f(n)=nとなり、それ以外のときは、f(n)≦n−2となります。
次に、n≧3のとき、nより小さい2のべき乗で最大のものをmとすると、f(n)=(n−m)×2・・・式A となります。さて、これをnに(2≦n)関して数学的帰納法により、証明してみます。
(はじめに)
n=3のとき、解答例2より、f(3)=2だから、式Aは成り立ちます。(帰納法の仮定) n=k(3≦k)のときに、式Aが成り立つと仮定します。
(n=k+1のとき)
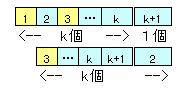
最初の1個(1の番号のボール)を取ります。残りは、k個です。
次は、残ったボールの2番目(3の番号のボール)を取ることになるので、残る2の番号のボールを最後尾に回すことにします。
もし、kが2のべき乗だとすると、仮定より、f(k)=kですので、最後尾の2の番号のボールが最後に残ることとなります。従って、f(n)=2となります。
また、n=k+1より小さくて最大の2のべき乗はkということになるので、m=k、従って、(n−m)×2=2となり、式Aは成立します。
もし、kが2のべき乗ではないものとすると、f(k)≦k−2なので、最後に残るボールは、最後の2個ではあり得ません。ボールは3からならんでいますので、結局f(k+1)=f(k)+2=(k−m)×2=(k+1−m)×2となります。
また、kが2のべき乗ではないので、n=k+1より小さくて最大の2のべき乗は、n=kのときのmに等しくなります。
よって、先ほどのf(k+1)=(k+1−m)×2は、n=k+1のときも式Aが成り立つことを意味します。
以上から、数学的帰納法により、3≦nの全てのnに関して式Aが成立することとなります。
以上