第118問の解答
1.問題 [速さ]
|
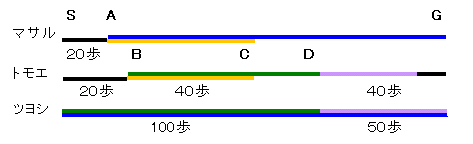
歩幅および歩を進めるペースがそれぞれ違う、マサル君、トモエさん、ツヨシ君の3人が公園の入口にいます。3人はそれぞれ一定の速度で公園を横切って、出口に向かうことにしました。 まず、マサル君とトモエさんが20歩ずつすすみました。そして、3人同時に“出発”したところ、トモエさんは“出発”後40歩進んだところでマサル君に追いつかれました。また、ツヨシ君は“出発”後100歩進んだところでトモエさんに追いつき、その後50歩進んだところでマサル君と同時に出口に到着したそうです。また、トモエさんはツヨシ君に追い抜かれてから40歩で出口に到着したそうです。 (1)3人の歩幅の比をマサル:トモエ:ツヨシの順で最も簡単な整数で答えてください。 (例:7:8:9) (2)公園の入口から出口までの距離は90mであったそうです。マサルさんの歩幅は何cmでしょうか。 |
2.解答例(H.Takaiさん、伏見主事さん、kuri他)
(1)3人の歩幅比
上図で、線分は歩いた距離を表し、同じ色の部分は同一時間であることを表すこととします。
まず、マサル君、トモエさんの出発点をA、Bとし、マサル君がトモエさんに追いついた地点をC、ツヨシ君がトモエさんに追いついた地点をDとします。
まず、SG間のツヨシ君の歩数は、100+50=150歩です。
すると、DH間のトモエさんの歩数は40歩、ツヨシ君の歩数は50歩です。
従って、SD間のトモエさんの歩数は、ツヨシ君の歩数100歩に対し、100*40/50=80歩と分かります。これから、CD間は、80−(20+40)=20歩となります。従って、トモエさんの歩数は、SG全体では、20+40+20+40=120歩と分かります。
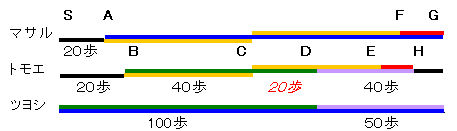
すると、ツヨシ君がSD間を100歩で進む時間に、トモエさんはBD間を60歩進むことになるので、ツヨシ君がDG間の50歩進む時間にトモエさんが歩くDH間の歩数は50×60/100=30歩となる。
さて、SC=CG=60歩なので、C地点は、ちょうどSとGの中間点となります。
最後に、SG間のマサル君の歩数を求めましょう。
そこで、FをGより20歩手前の地点とします。
C地点を軸として左右対称になっていることから、マサル君がFG間を歩いた時間にトモエさんが歩いた区間をEHとすると、CE=BC=40歩となります。
よって、EH=CH−CE=20+30−40=10歩となり、同じ時間にマサル君はトモエさんのちょうど倍の歩数を歩くことになります。
従って、トモエさんがBH間の90歩進む時間にマサル君はAG間を180歩進むことになるので、SG間では、20+180=200歩になります。
よって、SG間を歩く歩数は、マサル君:200歩、トモエさん:120歩、ツヨシ君:150歩となり、3人の歩幅の比は、200:120:150の逆数の比=3/600:5/600:4/600=3:5:4となります。
(2)マサル君の歩幅
マサル君は、SG=90mを200歩で歩くことになるので、歩幅は、90/200=0.45m=45cmとなります。
答:(1)3:5:4 (2)45cm
以上