第121問の解答
1.問題 [速さ]
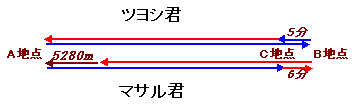
| マサルさんとツヨシ君が、町内マラソン大会に出場しました。A地点を出発して、B地点で折り返し、再び同じコースを通ってA地点にもどってくるマラソンです。 序盤で先行したツヨシ君は、先にB地点で折り返し、折り返してから5分後にマサル君とすれちがいました。 マサル君はその6分後にようやくB地点に到着しました。奮起したマサル君は、B地点に到着後、速さを1.1倍にしましたが、同じペースで走ったツヨシ君がゴールしたとき、マサル君はその後方5280mの地点を走っていました。 さて、このマラソンコースは全長何Kmでしょうか? |
2.解答例1(ありさのお父さん、ぶぶおパパ他)
ツヨシ君とマサル君がすれ違った地点をC地点とします。
まず、BC間をツヨシ君は5分、マサル君は6分で走るのだから、同一区間を走る2人の所要時間の比は、5:6である。
また、ツヨシ君がC地点でマサル君とすれ違う5分前にツヨシ君はB地点に到着しており、マサル君はそれより6分後にB地点に着くことから、AB間を走る2人のタイム差は、5+6=11分である。
従って、2人がAB間を走るときの所要時間は、ツヨシ君:11×5=55分、マサル君:11×6=66分となる。
よって、ゴールまでの合計時間は、ツヨシ君:55×2=110分、マサル君:66+60=126分となり、タイム差は126−110=16分である。
マサル君は、この16分で5280m走るのだから、BA間の60分では5.28/16×60=19.8Km走ることになるので、マラソンコースの長さは、19.8×2=39.6Kmである。
答:39.6Km
以上
3.解答例2(ぐっちさん、中村明海さん、kuri他)
AB間の距離をdKmとする、上記と同じ考え方で、往きでのツヨシ君とマサル君のスピード比は、6:5であるので、それぞれ6×V、5×Vとおくことができる。また、帰りは、ツヨシ君6×V、マサル君5×1.1×Vとなる。
従って、ちょうどツヨシ君がAB間を往復する時間は、
d/(6×V)×2=d/(5×V)+(d−5.28)/(5.5×V)
と表せるので、これを解いてd=19.8Kmを得る。従って、往復は39.6Kmとなる。
以上