第123問の解答
1.問題 [空間図形]
(図1)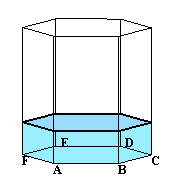 |
(図2)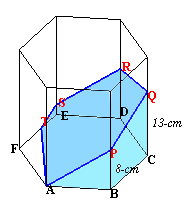 |
| (図1)のような正六角形ABCDEFを底面とする角柱の容器に水が入っています。
この容器を少し傾けたところ、(図2)のような状態になり、CQ=13cm、BP=8cmでした。(注:図2では、元の位置へ戻しています。) では、(図1)の状態のとき、水の高さは底面から何cm あったでしょうか。? |
2.解答例1(吉川マサルさん他)
(図3)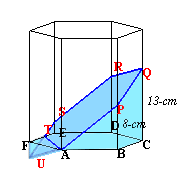 |
(図4)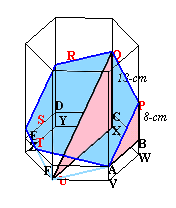 |
図3で、APQRSTが作る平面とFから真下に下ろした直線が交わる点をUとする。
次に、図4でUを通り底面ABCDEFに水平な面へA、B、C、D、Eから真下に下ろした点をV、W、X、Y、Zとする。
すると、△QUXと△PABは対応する各辺が平行であることから相似となる。また、UX=FC=2×ABより、相似比は2:1である。
よって、QX=2×AB=16cmとなり、FU=CX=QX−QC=16−13=3cmと分かる。
さて、R、Sの高さは次のようにして分かります。
まず、RからQXに下ろした垂線の足をX’とします。すると、△QRX’と△AUVは合同となり、QX’=AV=3cmとなります。よって、Rの高さはQより3cm低い10cmとなります。同様に、Sの高さは、Rの高さよりPB=8cm分だけ低くなるので10−8=2cmと分かります。
以上から、六角形APQRSUの対応する頂点の高さの平均は、(Aの高さ+Rの高さ)/2=(0+10)/2=5cm、(Pの高さ+Sの高さ)/2=(8+2)/2=5cm、(Qの高さ+Uの高さ)/2=(13−3)/2=5cmと全て5cmになります。
従って、もし三角錐UAFTに水が入っているものと考えれば、水面をならせば5cmの高さになると考えられます。
しかし、実際には三角錐UAFTに水は入っていないので、この体積分の高さを逆に加えてやる必要があります。
正六角形ABCDEFの面積を1とすると、三角形AEFの面積は1/6となります。また、ET:TF=SE:FU=2:3となるので、三角形AFTの面積=三角形AEFの面積×3/5=1/6×3/5=1/10と分かります。
よって、三角錐UAFTの体積=1/3×(1/10×3)=1/10となりますので、これを正六角形ABCDEFの面積1の広さにならすと高さは1/10=0.1cm分になります。
よって、求める高さは、5cm+0.1cm=5.1cmとなります。
答:5.1cm
以上
3.解答例2(たなかさん他)
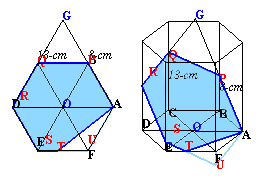
Rの高さを次のようにして求めます。
APとRQを延長して交わる点をGとします。すると、AP:AG=1:2になるので、Gの高さ=Pの高さ×2=16cmとなります。
同様に、RQ:RG=1:2なので、(Rの高さ+Gの高さ)/2=Qの高さとなり、Rの高さ=Qの高さ−(Gの高さ−Qの高さ)=13−(16−13)=10cmとなります。
あとは、解答例1と同様です。
以上