第124問の解答
1.問題 [場合の数]
| 色の違う10個の箱と、見分けのつかない3つのボールがあります。 このボールを10個の箱に入れるとき、入れ方は 何通りあるでしょうか? ただし、1つの箱に何個ボールを入れても構いません。 |
2.解答例1(武田 浩紀さん、中村 明海さん、563匹目のナキウサギさん他)
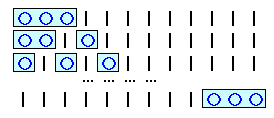
12個のマッチ棒を考えます。
このうち3個のマッチ棒を選びます。選び方は、12C3=12×11×10/(3×2×1)=220通りです。
残った9個のマッチ棒を仕切りと見て、選んだマッチ棒はボールに置き換えてみると、3個のボールを10個の箱に入れたことになるので、求める場合の数は220通りとなります。
答:220通り
(別解)
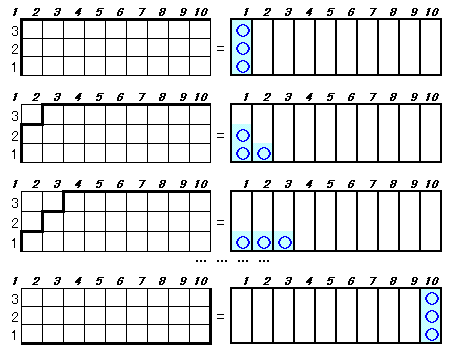
縦3行×横9列の格子を考えます。
左下隅から右上隅まで進む最短経路の数は、上へ進むことをN、右へ進むことをEと表すと、NNNEEEEEEEEE、NNENEEEEEEEE、・・・、EEEEEEEENNNなど3個のNと9個のEを重複を許して並べる順列の数=(3+9)!/(3!×9!)=12C3=220通りである。
以上
3.解答例2(柚奇神太郎さん、丸天後藤様、H.Takaiさん他)
場合分けで考えます。
1個ずつボールを入れる:
10個の箱より3個選ぶ・・・10C3=10×9×8/(3×2)=120通り2個入れる箱と1個入れる箱がある:
10個の箱より2個選び、さらにその2個より1個選んでそこへはボールを2個、他方へは1個入れる・・・10C2×2C1=10×9/2×2/1=90通り1箱にボールを3個入れる:
10個の箱より1個選ぶ・・・10C1=10/1=10通り合計220通り
以上