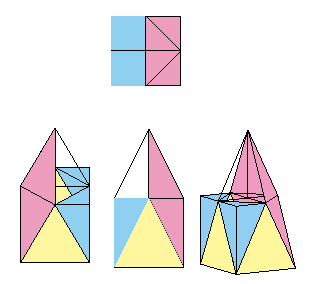第１２５問の解答

１．問題　［空間図形］

問題図
　左図のようなＡ、Ｂ、Ｃの各部品を使って、立体の展開図を作りました。

　Ａ、Ｂ、Ｃの各部品は、１辺の長さが６ｃｍの正方形を使って作りました。また、部品ＢおよびＣで、正方形の頂点以外の点は、正方形の辺の中点を用いています。

　では、この立体を組み立てたとき、 体積は何ｃｍ3になるでしょうか？

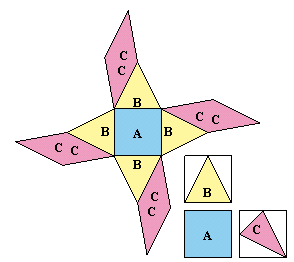
２．解答例１（ＴＯＲＡさん、わかさひ君、柚奇　神太郎さん他）

参考図１

（参考）立体図を自由に回転できるJavaアプレット
（柚奇　神太郎さん作）

部品Ｂが垂直に立っていることを示します。

参考図２

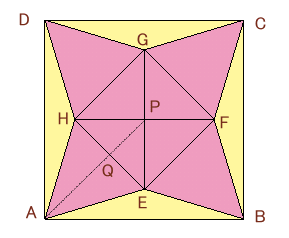
立体を真上から見た図を上記の通りとします。
すると、対象性から、四辺形ＥＦＧＨは正方形となり、ＥＦＧＨの作る平面は水平となります。

正方形ＥＦＧＨの中心をＯとすると、２等辺直角三角形ＯＥＨは、ちょうど部品Ｃを切り取って残る２等辺直角三角形と同じ大きさとなるので、結局ＥＦＧＨは、正方形ＡＢＣＤと同じ大きさの正方形となる。従って、部品Ｂの頂点Ｅ、Ｆ、Ｇ、Ｈは辺ＡＢ、ＢＣ、ＣＤ、ＤＡの真上にあることになり、言い換えれば部品Ｂが垂直に立っていることになります。

これから、点Ｅの高さは、部品Ｂの２等辺三角形の高さ、つまり部品Ａである正方形の１辺の長さ６ｃｍに等しくなる。また、頂点Ｐの高さ：点Ｑの高さ＝ＰＡ：ＱＡ＝２：１となり、点Ｑの高さは点Ｅの高さに等しいので、頂点Ｐの高さは、６ｃｍ×２＝１２ｃｍとなります。

参考図４

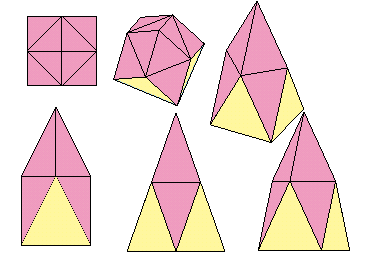
さて、面ＥＦＧＨで立体を輪切りにし、さらに上側の正４角錐をＥＧＰ、ＦＰＨを通る面で垂直に切り４等分にする。それらを逆さまにすると、ちょうど下側に残った立体のＡＨＥ、ＢＥＦの面などに置くと、立方体の角にぴったり収まるようになる。（上図は２個のみ置いたところ）

よって、求める立体の体積は、１辺が６ｃｍの立方体の体積に等しくなり、６×６×６＝２１６ｃｍ3となる。

答：２１６ｃｍ3

以上