第１２６問の解答

---

１．問題　［平面図形］

左図のような縦３ｍ、横６ｍのビリヤード台（長方形ＡＢＣＤ）があります。 　今、図のＳの位置にある玉を突いたところ、Ｒ、Ｑ、Ｐと跳ね返ってＢのポケットに入りました。 　Ｓは、Ｔから垂直に０．９ｍのところにあり、ＰＤ＝２ｍです。　 では、三角形ＳＢＰの面積を求めて下さい。

---

２．解答例１（ｋｕｒｉ他）

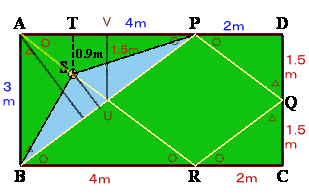
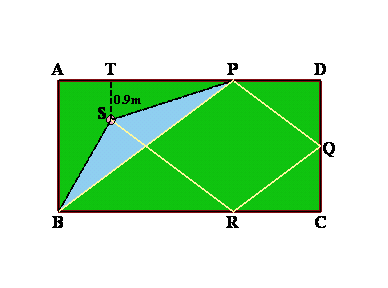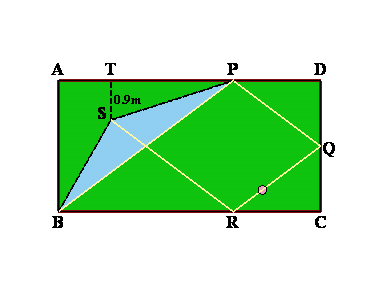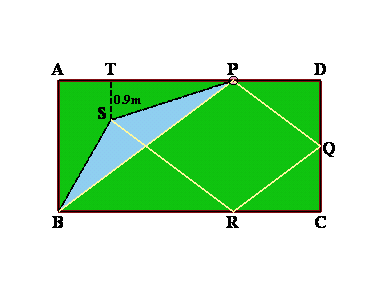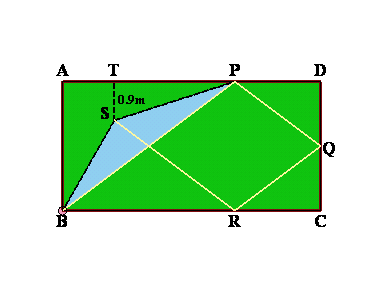
　玉が壁に当たって反射するとき、反射角が等しいことから、上図で○、△の角はそれぞれ等しい角となる。

　すると、△ＡＢＰと△ＤＱＰは相似となり、相似比はＡＰ：ＤＰ＝４：２。ＡＰ＝４ｍだから、ＤＱ＝ＡＢ×２／４＝１．５ｍ。よって、ＱＣ＝１．５ｍ。

　また、△ＣＱＲは△ＤＱＰと相似で、相似比はＣＱ：ＤＰ＝１．５：１．５＝１：１。
よって、ＣＲ＝ＤＰ＝２ｍとなり、ＢＲ＝４ｍと分かる。

　これから、△ＡＢＰと△ＢＡＲは合同となり、∠ＡＲＢ＝∠ＳＲＢ＝○だから、Ａ、Ｓ、Ｒは一直線上にあることが分かる。

　すると、対称性から、ＡＲとＢＰの交点Ｕは、直線ＡＤと直線ＢＣの中間点にあり、ＵＶ＝１．５ｍとなります。

　従って、△ＡＳＴと△ＡＵＶは相似で、相似比はＳＴ：ＵＶ＝０．９：１．５＝３：５。
よって、ＡＳ：ＡＵ＝３：５、ＳＵ：ＡＵ＝２：５になります。

　さて、△ＡＢＰと△ＳＢＰは、底辺がＢＰで共通、高さの比はＳＵ：ＡＵ＝２：５に等しい。

　よって、△ＳＢＰの面積＝△ＡＢＰの面積×２／５＝（１／２×３×４）×２／５＝２．４ｍ²となる。

答：２．４ｍ²

以上

---