第128問の解答
1.問題 [平均]
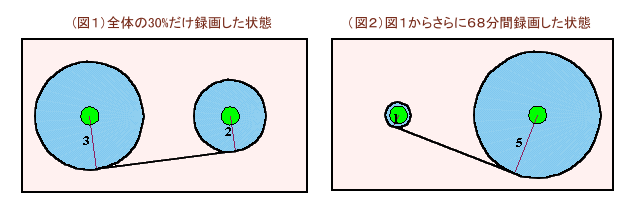
| ビデオテープがあります。 このビデオテープは、初めの状態では左側の芯にすべてのテープが巻かれており、右側の芯には巻かれていません。録画を行うと、右側のテープが左側のテープを徐々に巻き取っていきます。 このビデオテープに、録画可能時間の30%分だけ録画したところ、上の図1のように左円の半径:右円の半径=3:2になりました。 また、その後68分間録画してテープを見ると、上の図2のように、左円の半径:右円の半径=1:5になりました。 では、このビデオテープの録画可能時間は何分でしょうか? (注1)芯の半径は左右同じです。 |
2.解答例1(TORAさん、他多数)
下図のように考えると、テープの長さは、芯の部分をのぞいた円の面積に比例することが分かります。
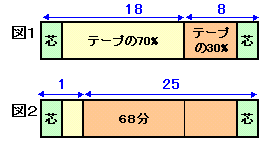
題意より、芯の分も含めて考えると、左の円の面積:右の円の面積は図1の時点で9:4、図2の時点で1:25となる。そこで、両方の芯の部分を含めた全体の長さを26とすると、下図のようになる。
図1から図2へ移った68分間分のテープの長さは18−1=17に相当する。従って、4分間分が 1に相当する。
また図1で、左のテープの長さから右のテープの長さの差を考えると、芯の部分は等しいので相殺されテープの40%の長さになります。これが、 18−8=10となるので40分となり、テープの全体の100%なら 100分となる。
なお、図1で左のテープだけの長さは30分、従って芯の長さは2分に相当することが分かる。
答:100分
以上
3.解答例2(ありさのお父さん、kuri他)
テープ全体の長さをL、芯の部分に相当する長さをL0とすると、上記と同じ考え方から次の式が得られる。
(L×0.7+L0) :(L×0.3+L0) =9:4 ・・・・(1)
(L×0.7+L0−68):(L×0.3+L0+68)=1:25 ・・(2)(1)より、L0=L/50となり、これを(2)に代入して、L=100を得る。従って、L0=2と分かる
以上