第129問の解答
1.問題 [速さ]
| 特急と快速がそれぞれ一定の間隔で走っている線路があります。 この線路沿いに、マサル君が自転車に乗って走ったところ、19分ごとに快速とすれちがい、また特急には38分ごとに追い抜かれました。 また、快速に乗っていたトモエさんは、特急と16分ごとにすれ違ったそうです。 では、特急に乗っていたツヨシ君は、 何分ごとに快速とすれ違ったでしょうか。 |
2.解答例1(柚奇 神太郎さん、長野 美光さん、H.Takaiさん他)
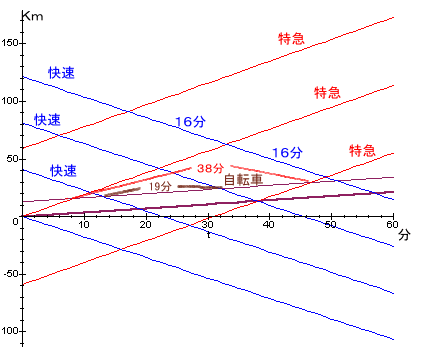
下図のようにダイアグラムを作成して考えます。
特急および快速はそれぞれ等間隔に一定速度で走っていますので、ダイアグラム上で特急と快速が出会う点は平行四辺形上にあります。
さえて、マサルさんの自転車が快速と出会うのが19分おき、特急に追い抜かれるのがその2倍の38分おき、ということから、ダイアグラム上でマサルさんの自転車が走る直線を原点(特急と快速が出会う点)まで平行移動すると上図のようになり、特急に一度追い抜かれて次ぎにまた追い抜かれるとき、ちょうど2台目の快速と出会うこととなります。
従って、その38分間の間に特急は2台の快速と出会い、その快速が次の特急に出会うことになります。
すなわち、特急が快速と出会うのは、(38−16)/2=11分おきとなります。
答:11分
以上
3.解答例2(中村明海さん、おりくん、kuri他)
特急、快速、自転車の速度をそれぞれV1,V2,V3Km/分、特急、快速の運転間隔をそれぞれL1、L2Km、および特急が快速と出会うのをT分おきとします。
題意から次の式が得られます。
(V1−V3)×38=L1 ・・・ (1)
(V2+V3)×19=L2 ・・・ (2)
(V1+V2)×16=L1 ・・・ (3)
(V1+V2)×T =L2 ・・・ (4)(1)、(2)より、V1=V3+L1/38、V2=−V3+L2/19を得るので、これを(3)に代入すると、
(V3+L1/38−V3+L2/19)×16=L1
(L1+L2×2)×16=L1×38
L1×(38−16)=L2×32
L2/L1=22/32 ・・・ (5)(4)/(3)より、
T/16=L2/L1
T=L2/L1×16=22/32×16=22/2=11
を得る。
以上
4.設問2(中村明海さんによる)
| 特急の運転間隔は快速の運転間隔より8分16秒長く、また特急の間隔は58.9Kmでした。 では、マサル君の自転車は時速何Kmでしょうか? |
解答例2に次の式が加わります。
L1/V1−L2/V2=8+16/60 ・・・ (6)
L1=58.9 ・・・ (7)
(5)、(7)より、
L2=L1×11/16=6479/160(6)に代入して、
58.9/V1-6479/160/V2=124/15
これと(3)より、V2を消去して、
1984/15×V1^2-311581/150×V1+346921/100 = 0V1=19/10、1767/128、このときV2=57/32、-6479/640、
V3=7/20、7843/640
2番目の解はV2が負となり不可。
よって、V3=7/20Km/分=7/20×60Km/時=21Km/時
答:21Km/時
以上