第１３０問の解答

---

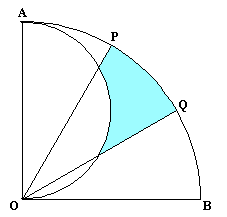
１．問題　［平面図形］

左図のようにＯを中心とする半径１２ｃｍ、中心角９０度の扇形があり、その中にＯＡを直径とする半円があります。 弧ＡＢの３等分点をＰ、Ｑとするとき、図の 水色で囲まれた部分の面積を求めて下さい。 円周率を３．１４として計算して下さい。

---

２．解答例１（長野　美光さん他多数）

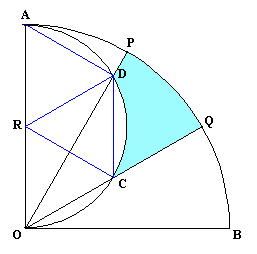
下図のように、ＡＢの中点をＲ、ＯＰおよびＯＱと弧ＡＢの交点をＤ、Ｃとします。

△ＲＯＣはＲＣ＝ＲＯ＝６ｃｍの２等辺三角形。∠ＲＯＣ＝６０度だから∠ＲＣＯ＝６０度となり△ＲＯＣは正三角形となります。

また、△ＡＲＤはＲＡ＝ＲＤの２等辺三角形。ところで、△ＡＤＯで∠ＡＤＯ＝９０度、∠ＡＯＤ＝３０度だから∠ＲＡＤ＝１８０度−（９０度＋３０度）＝６０度。よって、△ＡＲＤも正三角形。

よって、∠ＣＲＤ＝１８０度−（６０度＋６０度）＝６０度となり、△ＣＲＤも正三角形となります。

従って、ＣＤ＝ＲＤ＝６ｃｍで、ＣＤはＡＯに平行となります。

よって、△ＯＣＤと△ＲＣＤは、底辺がＣＤで共通、高さも等しいので面積が等しくなります。

従って、
扇形のようなＯＣＤの面積＝弓形ＣＤの面積＋△ＯＣＤの面積
　　　　　　　　　　　　　　　＝弓形ＣＤの面積＋△ＲＣＤの面積
　　　　　　　　　　　　　　　＝扇形ＲＣＤの面積

求める図形の面積＝扇形ＯＰＱの面積−扇形のようなＯＣＤの面積
　　　　　　　　　　　＝扇形ＯＰＱの面積−扇形ＲＣＤの面積
　　　　　　　　　　　＝π×１２²×３０／３６０−π×６²×６０／３６０
　　　　　　　　　　　＝π×６＝３．１４×６＝１８．８４ｃｍ²

　

　

答：１８．８４ｃｍ²

以上

---