第１３１問の解答

---

１．問題　［空間図形］

左図のような、半径３cmの球があります。 　この球の周りに、長さが全て同じ竹ひご６本でやぐらを組みました。このとき、すべての竹ひごは、球に接していました。 　この６本の竹ひごによって作られたやぐらの容積を求めてください。

---

２．解答例１（武田浩紀さん、モンゴルさん他多数）

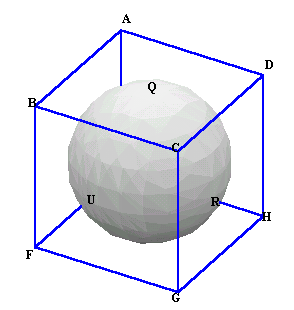
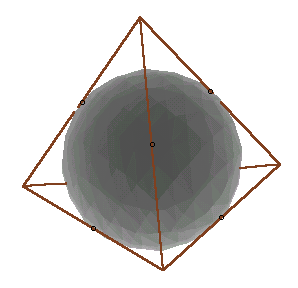
下図のように、球に外接する立方体を考えます。立方体の１辺は球の直径と同じ６ｃｍになります。ただし、Ｑ、Ｒ、Ｕは、球と立方体が接する点とする。例えば、Ｑは正方形ＡＢＣＤの中心である。

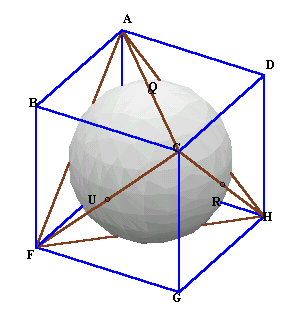
立方体の頂点Ａ、Ｃ、Ｆ、Ｈを結んで作る４面体は各辺の長さが全て等しい正四面体になる。そして、各辺の中点（Ｐ、Ｑ、Ｒ、Ｓ、Ｔ、Ｕ）は、立方体の各面の中心であることから、球に接しているので、これが求めるやぐらに他ならない。

　

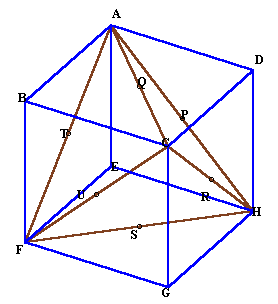
従って、やぐらの体積＝
　立方体の体積−（三角錘ＢＡＦＣ＋三角錘ＤＡＣＨ＋三角錘ＥＡＦＨ＋三角錘ＧＣＦＨ）
＝６×６×６−１／３×（１／２×６×６×６）×４＝（６−４）×６×６＝７２ｃｍ³となる。

答：７２ｃｍ³

以上

（参考）マウスでドラッグして下さい。

---

３．解答例２（ぶぶおパパさん、H.Takaiさん他多数）

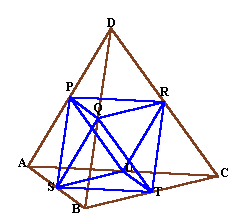
下図のように、正四面体の各辺の中点を結んでできる立体は、正八面体になります。

（参考）マウスでドラッグして下さい。

まず、この正八面体の体積を求めます。
正八面体を正方形ＰＳＴＲを通る平面で２つに切ります。
正方形ＰＳＴＲの対角線の長さはちょうど球の直径＝６ｃｍですから、面積は６×６／２＝１８ｃｍ²、Ｑから正方形ＰＳＴＲにおろした垂線の長さは球の半径＝３ｃｍ。
よって、正八面体の体積＝四角錐ＱＰＳＴＲの体積×２
　　　　　　　　　　　　　　　＝（１／３×１８×３）×２＝３６ｃｍ³

さて、正四面体から正八面体を除いた部分は、ＤＰＱＲなど同じ大きさの正四面体４個分であり、それぞれの正四面体は各辺の長さが元の正四面体の半分だから体積は１／８。
合計１／８×４＝１／２。

よって、求める正四面体の体積はちょうど正八面体の体積の２倍＝７２ｃｍ³となります。

以上

---

４．解答例３（長野義光さん、ｋｕｒｉ他多数）

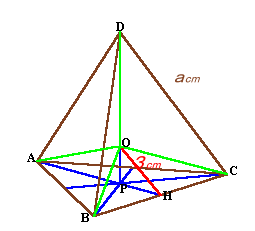
下図で正四面体の１辺の長さをａｃｍとします。

ＡＢ＝ａ、ＢＨ＝ａ／２より、ＡＨ＝√３／２×ａ、
ＰＢ＝ＡＰ＝ＡＨ×２／３＝√３／３×ａ。　(注１)
ＤＢ＝ａ、ＰＢ＝√３／３×ａより、ＤＰ＝√６／３×ａ、
ＯＰ＝ＤＰ／４＝√６／１２×ａ。　（注２）

よって、ＯＰ＝√６／１２×ａ、ＰＨ＝ＡＨ／３＝√３／６×ａより、
ＯＨ＝１／√８×ａ、ＯＨ＝球の半径＝３ｃｍなので、ａ＝√８×３＝√２×６ｃｍ。

さて、正四面体の体積＝１／３×正三角形ＡＢＣ×ＤＰ
　　　　　　　　　　　　　＝１／３×（１／２×ａ×√３／２×ａ）×√６／３×ａ
　　　　　　　　　　　　　＝√２／１２×ａ³＝７２ｃｍ³

以上

---