第１３５問の解答

第１３５問の解答

１．問題　［空間図形］

　左図は、それぞれのマスが一辺の長さ１cmの正方形である方眼紙の上に、ある立体の展開図を描いたものです。（※）

　この展開図を組み立てて出来る立体をいくつか使って、すきまなく組み合わせると、直方体を作ることができます。

　では、作ることのできる最も小さい直方体について、
　（１）体積
　（２）表面積
　を求めてください。

※・・・実線は切り取り線、点線は折り目を表しています。

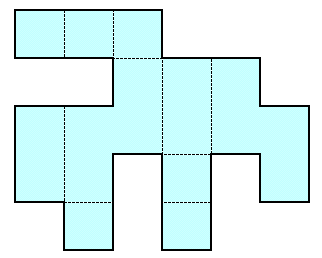２．解答例１（たなかさん、ありさのお父さん他）

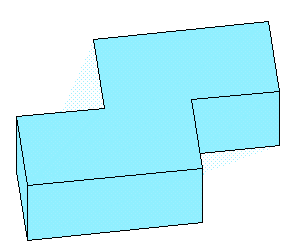
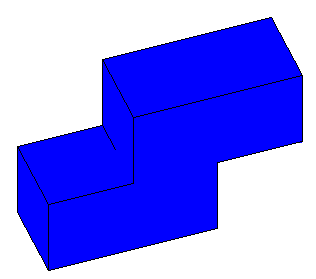
　展開図をもとに立体図を組み立てると下図のようになります。

タイプ１
タイプ２

　この立体を使ってできる直方体の縦×横×高さをａ×ｂ×ｃ（ａ≦ｂ≦ｃ）とする。

縦が１となるためには、タイプ１（上下ひっくりかえしたものを含む）のもののみで直方体を作る必要があるが、タイプ１はジグザグ型なので、どうやっても直方体の角を作ることができないので不可能である。

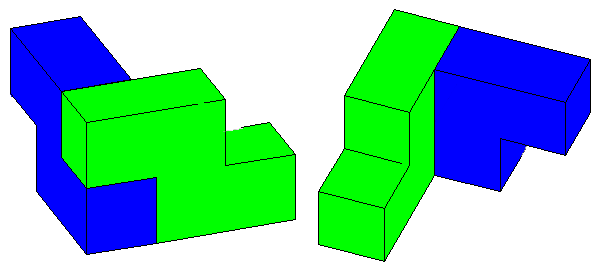
縦が２となるように、タイプ２のみで作ることも無理である。なぜなら、下図のようにタイプ２を２個組み合わせて直方体の角を作ったとすると、その内側にも角を作らないといけなくなるからである。

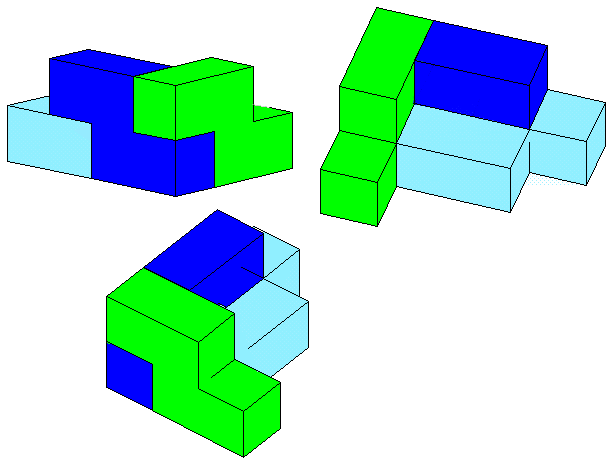
　そこで、タイプ１を１個とタイプ２を２個組み合わせて下図のようにする。

すると、ちょうど空いた部分にこの立体を上下ひっくり返したものをかぶせると２×３×４の直方体になることが分かる。

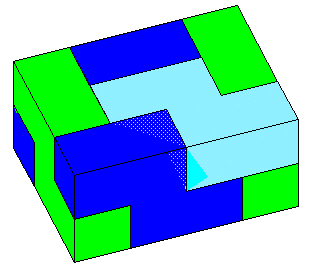［アニメＯＮ］を押すと直方体を作るようすをアニメで表示します。

　　

　

従って、求める直方体の体積＝２×３×４＝２４ｃｍ³、表面積＝（２×３＋３×４＋４×２）×２＝５２ｃｍ²。

答：（１）体積：２４ｃｍ³、（２）表面積：５２ｃｍ²

以上