第１４０問の解答

---

１．問題　［平面図形］

左図のような、ＡＢ：ＢＣ＝２：５の三角形ＡＢＣがあります。いま、角ＡＢＣの二等分線ＢＥをひき、さらに頂点Ｃから直線ＢＥに垂線ＣＤを下ろしました。 　このとき、三角形ＡＢＥと三角形ＤＥＣの面積比を求めてください。

---

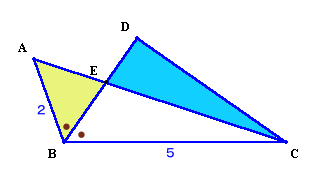２．解答例１（おりくん他）

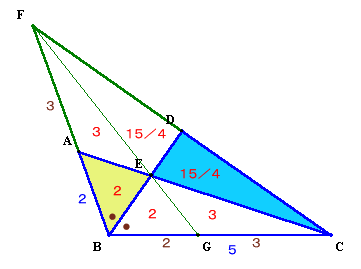
　BAの延長線とCDの延長線の交点をF、FEの延長線とBCとの交点をGとすると、
三角形ＢＦＣはＢＣを軸に対称になるので、ＡＦ＝ＧＣ＝３、ＢＧ＝ＢＡ＝２となる。

従って、△ABE:△AFE=ＢＡ：ＡＦ＝２：３、
　　　　△GBE:△GCE=ＢＧ：ＧＣ＝２：３、
　　　　△GFB:△GFC=ＢＧ：ＧＣ＝２：３。

よって、△GFC＝△GFB×３／２＝７×３／２＝２１／２、
　　　　△DCE＝（△GCE−△GCE）／２＝（２１／２−３）／２＝１５／４。

従って、△ABE:△DCE=２：１５／４＝８：１５になります。

答：８：１５

以上

---

３．解答例２（平野邦彦さん、真鍋豪仁さん、H.Takaiさん、たなかさん他）

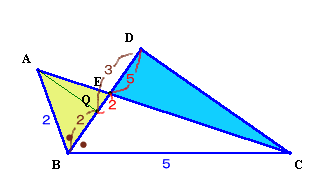
ＡからＢＤに垂線ＡＱをおろす。

すると、三角形ＡＢＱとＣＢＤは相似で相似比はＡＢ：ＢＣ＝２：５、
よって、ＢＱ：ＱＤ＝２：３。

また、三角形ＡＱＥとＣＥＤは相似で相似比はＡＱ：ＣＤ＝ＡＢ：ＢＣ＝２：５、
ＱＥ＝３×２／７、ＥＤ＝３×５／７、
ＢＥ：ＥＤ＝（ＢＱ＋ＱＥ）：ＥＤ＝（２０／７）：（１５／７）＝４：３。

従って、△ＡＢＥ／△ＤＥＣ＝（ＢＥ×ＡＱ）／（ＥＤ×ＣＤ）＝
　　　　＝（ＢＥ／ＥＤ）×（ＡＱ／ＣＤ）＝（４／３）×（２／５）＝８／１５。

よって、△ＡＢＥ：△ＤＥＣ＝８：１５。

---

４．解答例３（飯田孝久さん）

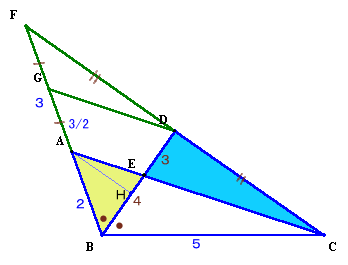
　BAの延長線とCDの延長線の交点をF、ＤからＢCに平行線を引きＢＦとの交点をGとすると、 三角形ＢＡＦとＢＤＣは合同、ＤＦ＝ＤＣ、ＢＦ＝ＢＣ＝５、　ＡＦ＝ＢＦ−ＢＡ＝３。

三角形ＦＡＣにおいて中線定理より、ＦＧ＝ＧＡ＝３／２。
三角形ＢＡＥとＢＧＤは相似、ＢＥ：ＥＤ＝ＢＡ：ＡＧ＝４：３。

また、三角形ＢＡＨとＢＣＤは相似、ＡＨ：ＣＤ＝ＢＡ：ＢＣ＝２：５。

よって、△ABE／△DCE=（ＢＥ×ＡＨ）／（ＥＤ×ＣＤ）
　　　＝（ＢＥ／ＥＤ）×（ＡＨ／ＣＤ）
　　　＝（４／３）×（２／５）＝８：１５。

---

５．解答例４（ｋｕｒｉ）

∠ABE＝∠ＣＢＥ＝θとおく。

△ABＣ＝1/2×ＡＢ×ＢＣ×sin２θ、△ABE＝1/2×ＡＢ×ＢＥ×sinθ、
△ＣＢE＝1/2×ＢＣ×ＢＥ×sinθ。

よって、△ABE：△AＣE＝ＡＢ：ＢＣ＝２：５、
　　　　△ABE＝2/7×△ABＣ、△ＣＢE＝5/7×△ABＣ。

△ＢＣＤ＝1/2×ＢＤ×ＣＤ＝1/2×（ＢＣ×cosθ）×（ＢＣ×sinθ）
　　　　　＝1/2×ＢＣ²×1/2×sin２θ
　　　　　＝1/2×ＢＣ／ＡＢ×△ABＣ
　　　　　＝５／４×△ABＣ。

従って、△ＤＥＣ＝△ＢＣＤ−△ＣＢE
　　　　　　　　　＝（５／４−５／７）×△ABＣ
　　　　　　　　　＝１５／２８×△ABＣ。

よって、△ABE：△ＤＥＣ＝（２／７）：（１５／２８）＝８：１５。

---