第１４１問の解答

---

１．問題　［空間図形］

左図のような、直方体ＡＢＣＤ-ＥＦＧＨの内部に、長方形ＡＢＣＤの中心（対角線の交点）を頂点とする四角すいＯ−ＥＦＧＨを作ったものです。 　３点Ａ、Ｆ、Ｐ（ＰはＤＣの中点）を通る平面でこの直方体および四角すいを切断するとき、四角すいＯ−ＥＦＧＨはア：イの体積比で分けられます。 　このとき、ア、イにあてはまる数を求めてください。ただし、ア＞イとします。

---

２．解答例１（たなかさん、あれふさん他）

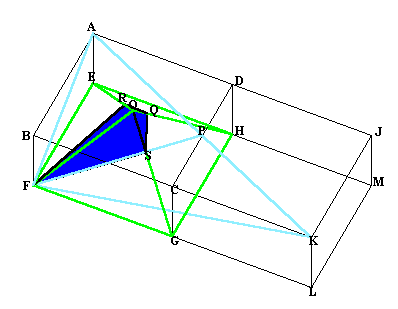
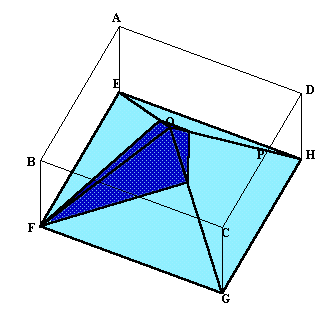
まず最初に平面AFPはCGの中点Mを通ることがわかります。

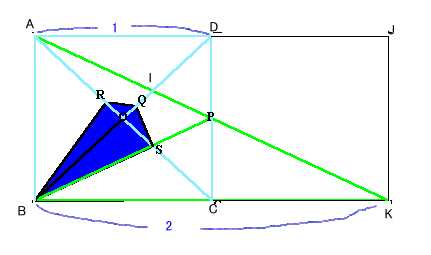
APとBDの交点をIとすると、△ＡＩＤと△ＫＩＢが相似で相似比１：２からBI:ID=2:1がわかります。

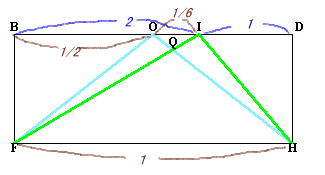
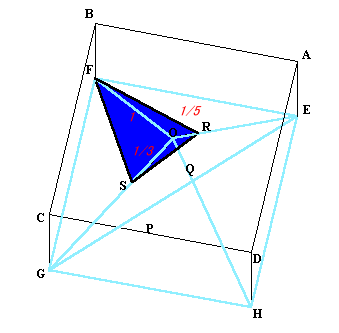
ここで、BFHDの断面を考えると、線分OHと平面APFの交点Qは、OHとIFの交点になります。この断面図で△ＯＱＩと△ＨＦＱの相似比を考えると、OQ:QH=1:6が求まります。

次に断面AEGCを考えます。

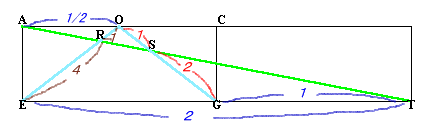
平面AFPと線分OE,OGの交点をそれぞれR,Sとすると、これらは線分AＴとOE,OGの交点になります。前と同様に△ＡＲＯと△ＴＲＥおよび△ＡＳＯと△ＴＳＧの相似比によりOR:RE=1:4,OS:SG=1:2とわかります。
また、この断面図で△ＯＲＳ／△ＯＥＧ＝１／５×１／３＝１／１５がわかります。

全体の図形を今の断面AEGCでわけてこの面を底面と考えるましょう。

すると、この面よりＢ側で切り分けられた三角錐Ｆ−ＯＳＲは三角錐Ｆ−ＯＧＥに比べ底面の面積比が１／１５、高さが同じなので体積比は１／１５です。

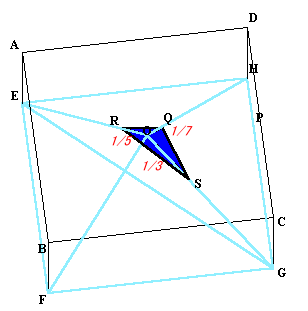
Ｄ側では、三角錐Ｑ−ＯＳＲは三角錐Ｑ−ＯＧＥに比べ底面の面積比が１／１５、高さが１／７なので体積比は１／１５×１／７＝１／１０５です。

従って立体ＯＲＦＳＱの体積は四角錐Ｏ−ＥＦＧＨの半分の１／１５＋１／１０５＝８／１０５、よって四角錐Ｏ−ＥＦＧＨの４／１０５と分かります。

よって、ＡＦＰで分かられる２つの立体の体積比は１０１：４となります。

答：１０１：４

以上

---

３．解答例２（長野　美光さん、中村明海さん他）

簡単のためにＡＢＣＤは正方形で、直方体の高さＡＥはＡＢの半分とします。
Ｏを原点に座標を下図のようにします。

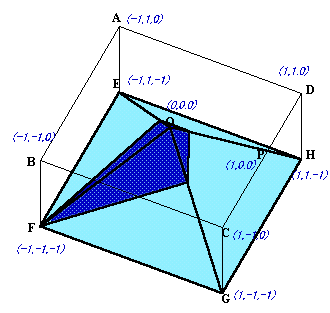
平面ＡＦＰは三点Ａ（−１，１，０）、Ｆ（−１，−１，−１）、Ｐ（１，０，０）を通ることから
ｘ＋２ｙ−４ｚ＝１となることが分かります。

また、四角錐の斜面ＯＥＦ、ＯＦＧ、ＯＧＨ、ＯＨＥは、
それぞれｚ＝ｘ、ｚ＝ｙ、ｚ＝−ｘ、ｚ＝−ｙとなります。

これから、ＡＦＰとＯＥの交点Ｒは、
　　ｘ＋２ｙ−４ｚ＝１、ｚ＝ｘ、ｚ＝−ｙより（-1/5,1/5,-1/5)、
ＡＦＰとＯＦの交点は、
　　ｘ＋２ｙ−４ｚ＝１、ｚ＝ｘ、ｚ＝ｙより（-1,-1,-)すなわちＦと同じ、
ＡＦＰとＯＧの交点Ｓは、
　　ｘ＋２ｙ−４ｚ＝１、ｚ＝y、ｚ＝−xより（1/3,-1/3,-1/3)、
ＡＦＰとＯＥの交点Ｑは、
　　ｘ＋２ｙ−４ｚ＝１、ｚ＝-ｘ、ｚ＝−ｙより（1/7,1/7,-1/7)
と分かります。

よって、ＯＲ、ＯＦ、ＯＳ、ＯＱの長さはＯＥの１／５，１，１／３，１／７となります。

あとは解答例１と同じ。

---