第１４２問の解答

１．問題　［平面図形］

問題図
　左の図のような、ＡＢ＝９cm、ＢＣ＝１０cm、ＣＡ＝１２cmの三角形ＡＢＣがあります。

　いま、角ＢＡＣの二等分線と、角ＢＣＡの二等分線をひき、それぞれに対して頂点Ｂから垂線ＢＱ、ＢＰをおろしました。

　このとき、ＰＱの長さを求めてください。

２．解答例１（長野　美光さん他）

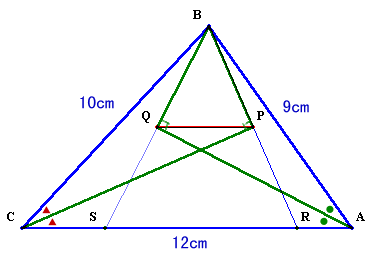
ＢＰ、ＢＱを延長し辺ＣＡとの交点をそれぞれＲ、Ｓとします。

参考図


すると、三角形ＡＢＳは二等辺三角形となり、ＡＳ＝ＡＢ＝９ｃｍ、ＢＱ＝ＳＱ、ＣＳ＝ＣＡ−ＡＳ＝１２−９＝３ｃｍがわかります。
同様に、三角形ＣＢＲは二等辺三角形となり、ＣＲ＝ＣＢ＝１０ｃｍ、ＢＰ＝ＲＰ、ＡＲ＝ＣＡ−ＣＲ＝１２−１０＝２ｃｍとなります。

よって、ＲＳ＝ＣＡ−ＣＳ−ＡＲ＝１２−３−２＝７ｃｍとなり、中点連結定理よりＰＱ＝ＲＳ／２＝７／２ｃｍとなります。

答：７／２ｃｍ

以上