第１４４問の解答

---

１．問題 ［場合の数］

左図の実線部分は、Ａ地点とＢ地点の間の道路を示しています。この道路は縦３マス、横４マスの碁盤の目状につながっており、それぞれのマスは全て正方形です。 　いま、Ａ地点からマサルさんがＢ地点に向かって、Ｂ地点からトモエさんがＡ地点に向かって同時に出発し、２人とも同じ速度で、かつ最短距離で進み、目的地に到着します。 　このとき、２人が出会う場合は何通りあるでしょうか。

---

２．解答例１（しぶあきさん、ありさのお父さん、中村明海さん）

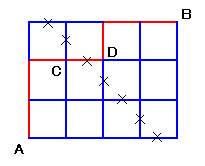
２人が出会う地点は、上図のように７個所あります。

例えば、３番目の地点で出会うために、マサルさんはＡＣを最短路で進み、ＣＤを通って、ＤＢを最短路で進みます。従って、進み方は₃C₂×₃C₂＝９通り。
同様にトモエさんは、ＢＤ、ＤＣ、ＣＡと進むので、₃C₂×₃C₂＝９通りで、併せて９×９＝８１通りあります。

同様に、７個所全部の出会う場合の数を加えると、
　（₃C₀×₃C₀）²×２＋（₃C₀×₃C₁）²×２＋（₃C₂×₃C₂）²×３
　＝１²×２＋３²×２＋９²×３＝２６３
通りになります。

答：２６３通り

以上

---