第１４５問の解答

１．問題　［平面図形］

問題図
　左図は、三角形ＡＢＣの角Ｂ、角Ｃの二等分線の交点をＤとし、Ｄを通りＢＣに平行な直線がＡＢ、ＡＣと交わる点をＥ、Ｆとしたものです。

　すると、三角形ＥＤＢ＝１７cm2、三角形ＤＢＣ＝４０cm2、三角形ＤＦＣ＝１５cm2となりました。

　このとき、三角形ＡＥＦの周の長さと、四角形ＥＢＣＦの周の長さの比を求めてください。

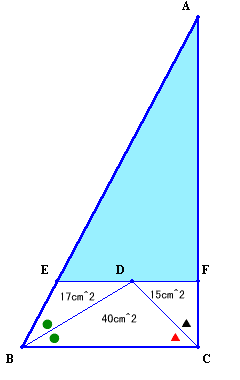２．解答例１（H.Takaiさん、Asamiさん、ｋｕｒｉ他）

参考図

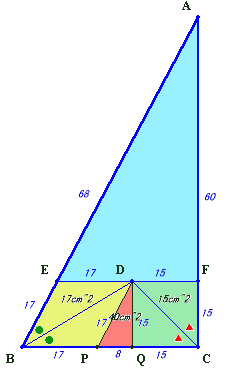
ＤからＢＣ上の点Ｐ、ＱをＥＢおよびＦＣと平行となるようにとる。

ＢＤ、ＣＤは∠ＥＢＰ、∠ＦＣＱの２等分線だから、平行四辺形ＥＢＰＤ、ＤＱＣＦは菱形となる。

従って、三角形ＢＰＤ＝１７ｃｍ2、三角形ＣＱＤ＝１７ｃｍ2。
よって、三角形ＤＰＱ＝４０−１７−１５＝８ｃｍ2。

これら３つの三角形は高さが共通だから底辺の比は面積比に等しい。
よって、ＢＰ：ＰＱ：ＱＣ＝１７：８：１５。
従って、ＥＢ＝ＥＤ＝ＢＰ＝１７、ＦＤ＝ＦＣ＝ＱＣ＝１５。

さて、三角形ＡＥＦと三角形ＡＢＣは相似で相似比は３２：４０＝４：５。
よって、ＡＥ：ＥＢ＝ＡＦ：ＦＣ＝４：１。
従って、ＡＥ＝ＥＢ×４＝１７×４＝６８、ＡＦ＝ＦＣ×４＝１５×４＝６０。

以上から、三角形ＡＥＦの周の長さ＝６８＋６０＋３２＝１６０、四角形ＥＢＣＦの周の長さ＝１７＋４０＋１５＋３２＝１０４。比は、１６０：１０４＝２０：１３。

答：２０：１３

以上