第１４７問の解答

１．問題　［平面図形］

　１cm、２cm、３cm、４cm、５cm、６cmの竹ひごが１本ずつあります。

　これを使って内角の大きさが全て等しい６角形を作ります。

　このとき出来る６角形は２種類ありますが、その面積比を「大きい方：小さい方」の順で答えてください。

２．解答例１（中村明海さん、ｋｕｒｉ他）

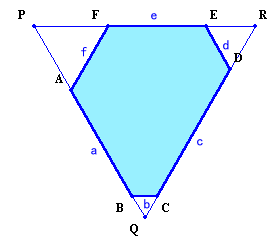
　下図のように、各辺に記号をつけます。
各内角は１２０度となり、向かい合う２辺は互いに平行となります。
従って、下図のごとく辺を延長してできる三角形は正三角形になる。

図１
参考図

ＡとＤの水平距離から、ａ／２＋ｂ＋ｃ／２＝ｄ／２＋ｅ＋ｆ／２　・・・　（１）。
ＢとＦ、ＣとＥの垂直距離から、ａ＋ｆ＝ｃ＋ｄ　・・・　（２）
（２）と同様に、ｂ＋ｃ＝ｅ＋ｆ　となるので、ａ－ｄ＝ｃ－ｆ＝ｅ－ｂ　・・・　（３）。

（１）より、
　ａ＋ｃ－（ｄ＋ｆ）＝２×（ｅ－ｂ）　　・・・　（４）

両辺は偶数となるが、ａ、ｂ、・・、ｆは奇数が３個、偶数が３個あります。
よって、ａ、ｃ、ｄ、ｆには奇数と偶数の個数は同じ２個づつあります。
従って、ｅ、ｂの一方は奇数、もう一方は偶数となります。

同様にして、全ての向かい合う辺の長さは奇数と偶数の組み合わせになります。

さて、ｂ＝１としましょう。
すると、向かいの辺は、ｅ＝２，４，６のいずれかとなります。

ｅ＝２のとき、（３）より、ａ－ｄ＝ｃ－ｆ＝１。
ａ，ｄ，ｃ，ｆは３，４，５，６のいずれかとなるので、
　ａ＝４、ｄ＝３、ｃ＝６、ｆ＝５またはａ＝６、ｄ＝５、ｃ＝４、ｆ＝３。

ｅ＝４のとき、（３）より、ａ－ｄ＝ｃ－ｆ＝３。
ａ，ｄ，ｃ，ｆは２，３，５，６のいずれかとなるので、
　ａ＝５、ｄ＝２、ｃ＝６、ｆ＝３またはａ＝６、ｄ＝３、ｃ＝５、ｆ＝２。

ｅ＝６のとき、（３）より、ａ－ｄ＝ｃ－ｆ＝５。
ａ，ｄ，ｃ，ｆは２，３，４，５のいずれかとなるので、差が５となる組み合わせはないので不適。

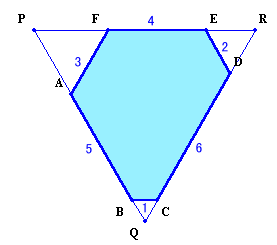
従って、題意に適する６角形は回転、対称となるものを除けば、下図の２通りとなる。

参考図２　参考図３

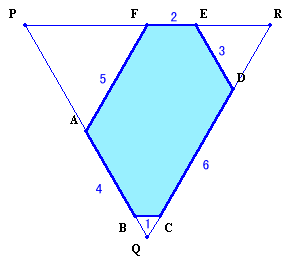
６角形の面積は、大きい正三角形から３隅の小さな正三角形の面積を引いたものとなるので、（１０²－１²－３²－５²）：（９²－１²－２²－４²）＝６５：６７

答：６７：６５

以上

３．解答例２（ｋｕｒｉ）

図１より、正三角形の１辺をＬとすると、ｆ＋ａ＋ｂ＝ｂ＋ｃ＋ｄ＝ｄ＋ｅ＋ｆ＝Ｌ。
加えると、ａ＋ｂ×２＋ｃ＋ｄ×２＋ｅ＋ｆ×２＝Ｌ×３、
よって、（ａ＋ｂ＋ｃ＋ｄ＋ｅ＋ｆ）＋（ｂ＋ｄ＋ｆ）＝Ｌ×３、
従って、ｂ＋ｄ＋ｆ＝Ｌ×３－（ａ＋ｂ＋ｃ＋ｄ＋ｅ＋ｆ）＝Ｌ×３－２１。

これから、ｂ＋ｄ＋ｆは３の倍数となります。
ｂ＝１、ｄ＜ｆとすると、（ｄ、ｆ）＝（２、３）、（２、６）、（３、５）、（５、６）。

　Ｌ＝（（ｂ＋ｄ＋ｆ）＋２１）／３より、
（ｄ、ｆ）＝（２、３）のときＬ＝９、（ａ、ｃ、ｅ）＝（５、６、４）　
（ｄ、ｆ）＝（２、６）のときＬ＝１０、（ａ、ｃ、ｅ）＝（３、７、４）・・・　不適
（ｄ、ｆ）＝（３、５）のときＬ＝１０、（ａ、ｃ、ｅ）＝（４、６、２）
（ｄ、ｆ）＝（５、６）のときＬ＝１１、（ａ、ｃ、ｅ）＝（４、５、０）・・・　不適

以下同様。

４．解答例３（ちばけいすけさん）

（１）より、ｂ×２＋ａ＋ｃ＝ｅ×２＋ｄ＋ｆ。

ｂ＝１、ａ＜ｃ、ｄ＜ｆとして考える。
左辺の取りうる値は、最小：１×２＋３＋４＝７、最大：１×２＋５＋６＝１３、
右辺の取りうる値は、最小：２×２＋３＋４＝１１、最大：６×２＋４＋５＝２１。
従って、両辺の値は、１１、１２、１３のいずれかとなる。

１１のとき、（ａ、ｃ）＝（４、５）または（３、６）、（ｅ、ｄ、ｆ）＝（２、３、４）・・・　不適。

１２のとき、（ａ、ｃ）＝（４、６）、（ｅ、ｄ、ｆ）＝（２、３、５）または（３、２、４）・・・後者は不適。

１３のとき、（ａ、ｃ）＝（５、６）、（ｅ、ｄ、ｆ）＝（２、３、６）、（２、４、５）、（３、１、６）、（３、２、５）、（４、２、３）・・・最後のみ適。