第１４９問の解答

---

１．問題　［平面図形］

左図のような、ＡＢ＝１２cm、ＣＤ＝１０cm、∠ＡＢＣ＝８０゜、∠ＢＣＤ＝７０゜の四角形ＡＢＣＤがあります。 　いま、辺ＡＤ、対角線ＢＤ、辺ＢＣ、対角線ＡＣの中点をそれぞれＰ、Ｑ、Ｒ、Ｓとします。 　このとき、四角形ＰＱＲＳの面積を求めてください。

---

２．解答例１（長野美光さん、ありさのお父さん、田村 稔さん、563匹目のナキウサギさん他）

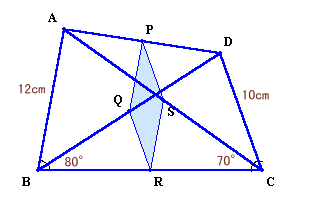
　△ＤＡＢについて、中点連結定理より、ＡＢとＰＱは平行でＰＱ＝ＡＢ／２＝６ｃｍ。
また、△ＣＡＢについて、中点連結定理より、ＡＢとＳＲは平行でＳＲ＝ＡＢ／２＝６ｃｍ。
よって、ＰＱとＳＲは平行でＰＱ＝ＳＲ＝６ｃｍ。

同様にして、ＰＳとＱＲは平行でＰＳ＝ＱＲ＝５ｃｍ。

よって、四角形ＰＱＲＳは平行四辺形となる。

さて、∠ＱＲＢ＝∠ＤＣＢ＝７０°、∠ＳＲＣ＝∠ＡＢＣ＝８０°、
よって、∠ＱＲＳ＝１８０−（７０＋８０）＝３０°。　

従って、平行四辺形の面積＝２×1/2×ＱＲ×ＳＲ×sin３０°＝５×６×1/2＝１５ｃｍ²。

答：１５ｃｍ²

（別解）平行四辺形ＰＱＲＳの面積

ＱからＲＳに垂線ＱＴを下ろします。
∠ＱＲＳ＝３０°より、△ＱＲＴは正方形の半分、よってＱＴ＝ＱＲ／２＝２．５ｃｍ。
従って、平行四辺形ＰＱＲＳ＝△ＱＲＳ×２＝1/2×６×２．５×２＝１５ｃｍ²。

以上

---