第152問の解答
1.問題 [場合の数]
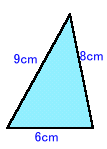 |
|
2.解答例1
(T.Endoさん、こだまさん、いおんとらんぷさん、takashiさん、伏見主事さん、おりくん、中村明海さん他)
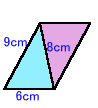
与えられた三角形を2個用いて、8cmの辺を共通に図1のように並べると平行四辺形になる。
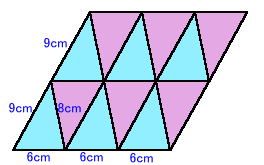
さらに、この平行四辺形の2辺の最小公倍数を求めて、図2のように並べると菱形となる。図2では、三角形を12枚並べることとなる。
図1
図2
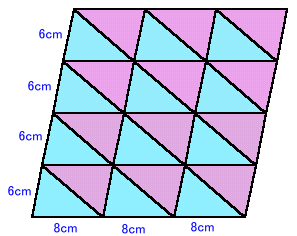
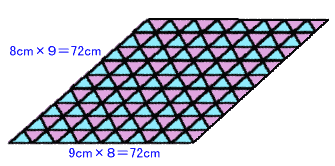
この他に9cmの辺を共通に並べた場合は24枚(図3)、6cmの辺を共通に並べた場合は144枚(図4)となります。
図3
図4
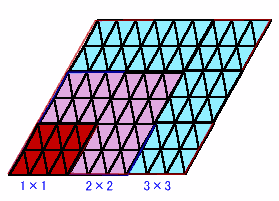
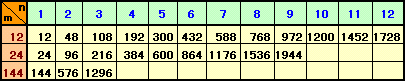
今度は、図5のように今求めた菱形を縦、横同じ個数並べても菱形となるので、2000枚以内でどれだけ並べられるかを求めると図6のようになる。
図5
図6
(ただし、m:最小の菱形での三角形の枚数、n:縦・横並べる個数)これらの中に重複するものはないので、12+9+3=24種類が求める個数である。
答:24種類
以上