第153問の解答
1.問題 [推理算]
| 次のようなゲームをしました。 1.マサル君がサイコロを2回ふる。このとき、大きいほうの出目をA、小さい方の出目をBとして覚えておく。(同じ出目なら、AとBは同じ数になります) 2.マサル君はA−Bの計算結果をW君に、A÷Bの計算結果から(もし小数になったら)小数を切り捨てた数をYさんに教える。(※) その後、W君とYさんの間では次のような会話がかわされました。 W君 「ん〜、差だけじゃ分からないな〜」 Yさん「差をしってるW君が分からないのね。えっと....でも私も分からないわ。」 W君 「A÷Bの整数の部分を知ってるYさんも分からないということは..... そうか、分かった!」 Yさん「あ、W君が分かったのなら、私も分かったわ。」 さて、サイコロをふって出たA、Bの数はそれぞれいくつだったでしょうか。 ※・・・このお二人はすご〜〜く賢いことで知られています。(^^;;。 |
2.解答例1
(長野 美光さん、takashiさん、柚奇
神太郎さん、わかさひ君、中村明海さん、H.Takaiさん、伊藤 建志さん他)
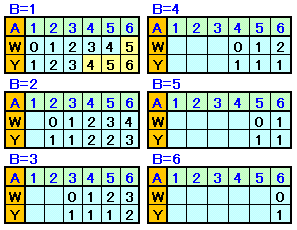
A、Bの各組み合わせに対してW(差)、Y(商)の値は下表のとおりとなる。
このうち、W=5であれば(A、B)=(6、1)しかないので、Wの第1発言「分からない」に反するのであり得ない。
また、Yの第1発言「私も分からない」ことから、Y=4,5,6の場合は除かれる。
これを聞いたWの第2発言「Yさんも分からないなら分かった」ことから、今除かれたY=4,5,6の場合のいずれかであるとは気づいたことになる。
すなわちW=3,4のいずれかとなる。W=3の場合、(W、Y)=(3、2)の組み合わせが(A、B)=(4、1)、(5、2)の2ケース残るのであり得ない。
W=4の場合、(W、Y)=(4、5)の組み合わせが(A、B)=(5、1)の1ケースと(W、Y)=(4、3)の組み合わせが(A、B)=(6、2)の1ケースあったが、Yの第1発言から前者は除かれるので、結局後者の(A、B)=(6、2)と分かる。答:(A、B)=(6、2)
以上