第155問の解答
1.問題 [やりとり算]
| マサルさんとトモエさんが、コインを使ってゲームをしました。じゃんけんをして、勝った方は、負けた方の持っているコインの半分をもらえるというゲームです。 最初、2人とも64枚ずつ持ち、6回勝負したところ、マサルさんのコインは79枚になったそうです。(引き分けはありませんでした) では、マサルさんから見て、2人の勝負はどのような結果だったのでしょうか。 「勝ちを1、負けを0」として、例えば、「勝ち−負け−負け−負け−勝ち−勝ち」ならば、「100011」と答えてください。 |
2.解答例1(長野 美光さん、popopoさん、CRYING DOLPHINさん他多数)
一回じゃんけんする前の2人のコイン数をx、y枚、じゃんけんした後のコイン数をx’、y’枚とします。
x枚持っているほうが勝ったことにすると、x’=x+y×1/2、y’=y×1/2となります。
このときx’−y’=x、y=y’×2を得るが、x’−y’=x>0より、x’>y’。すなわち、じゃんけん後のコイン数の多い方がじゃんけんを勝ったことになり、じゃんけん前のコイン数も一意的に決まります。
以上より、最終結果から逆にたどっていくと下記の通りとなるので、マサルさんは「勝ち−勝ち−勝ち−負け−負け−勝ち」すなわち「111001」と分かります。
答:111001
以上
3.解答例2(おりくん、kuri他)
2進数に関係しそうなことは容易に推測できますので、勝ち負けのパターンと最終コイン数の結果を比較して、関連をみてみましょう。
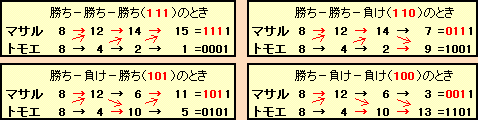
問題を簡単にするため、最初のコイン数を8枚、じゃんけんする回数を3回として、ケースごとの結果を下記に示します。ただし、最初はマサルさんが勝つものとします。
上図より、最終コイン数(2進数)の1位を除く部分を逆にしたものが勝ち負けのパターンとなっています。
これから、マサルさんの最終コイン数79を2進数にすると1001111となるので、勝ち負けのパターンは111001と予想されます。
これを検証してみましょう。
解答例1と同様にx、y、x’、y’の2進数表現を考えます。
例えば、x=98(11000102)、y=30(00111102)に対して、xが負けたとすると
x’=x×1/2=49(01100012)、
y’=y+x×1/2=(x+y)×1/2+y×1/2=64+y×1/2=79(10011112)
より、負けた方は右に1桁シフトし左に0を加える、勝った方は右にシフトし左に1を加える計算になります。従って、マサルさんの最終コイン数79(10011112)から見て、一番上位の1は6回目に勝ち、次の00は5回目、4回目に負け、次の111は3回目、2回目、1回目に勝ちを意味することと分かります。
すなわち、1位の1を除いたものを逆にしたものが勝ち負けのパターンになっています。