第１５７問の解答

１．問題　［平面図形］

問題図
左図のようなＡＢ＝６cmの三角形ＡＢＣがあります。
　ＡＣの中点をＭ、ＢＣの中点をＮとして、ＡとＮ、ＢとＭを結んだところ、２つの直線は垂直に交わったそうです。
　では、２つの直線の交点をＰとすると、ＰＣの長さは何cmでしょうか。

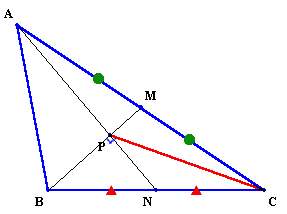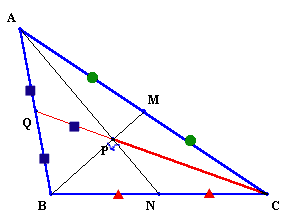
２．解答例１(伊藤建志さん、H.Takaiさん、モンゴルさん他)：Ｐが重心であることを利用

題意より、Ｐは三角形ＡＢＣの重心となります。

参考図１

従って、ＣＰを延長しＡＢと交わる点をＱとすると、ＱもＡＢの中点となります。

また、三角形ＡＢＰは直角三角形なのでＰＱ＝ＡＱ＝ＢＱ（Ｑは三角形ＡＢＰの外心）

さらに、Ｐは三角形ＡＢＣの重心だからＱＰ：ＰＣ＝１：２。
よって、ＰＣ＝ＱＰ×２＝ＡＢ＝６ｃｍとなります。

答：６ｃｍ

以上

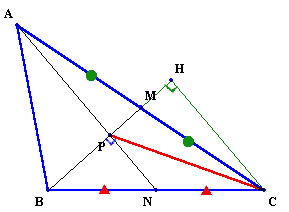
３．解答例２(わかさひ君、ｋｕｒｉ他)：算数的解法

ＣからＢＭの延長線上に垂線を下ろし、足をＨとします。

参考図２

三角形ＢＣＨについてＮＰとＣＨは平行でＮがＢＣの中点だから中点連結定理により、ＢＰ＝ＰＨ。

また、直角三角形ＡＰＭとＣＨＭは、∠ＡＰＭ＝∠ＣＨＭ＝直角、∠ＡＭＰ＝∠ＣＭＨ（相対する角）、およびＡＭ＝ＣＭより合同、よって、ＡＰ＝ＣＨとなります。

従って、直角三角形ＡＢＰとＣＰＨについて、ＢＰ＝ＰＨ、ＡＰ＝ＣＨだから合同、よってＰＣ＝ＡＢ＝６ｃｍとなります。

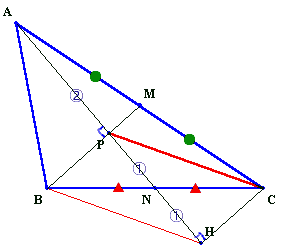
４．解答例３(極北の森さん、シイサン他)：算数的解法

ＰＮの延長線上にＰＮ＝ＮＨとなるようＨをとる。

参考図３

ＰＮ＝ＮＨ、ＢＮ＝ＮＣより、三角形ＰＢＮとＨＣＮおよびＨＢＮとＰＣＮは合同。
よって、ＰＢＨＣは平行四辺形となります。

従って、三角形ＡＨＣについてＡＭ＝ＭＣおよびＰＭとＨＣが平行だから、中点連結定理により、ＡＰ＝ＰＨ。

よって、直角三角形ＡＢＰとＰＣＨは、ＡＰ＝ＰＨ、ＢＰ＝ＣＨより合同。
従って、ＰＣ＝ＡＢ＝６ｃｍ。

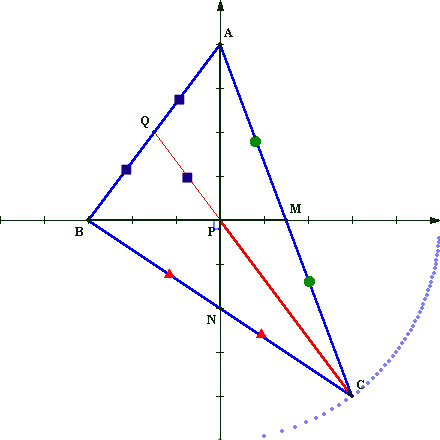
（参考）直線BMをX軸、直線ANをY軸とするXY平面を考える（大西俊郎さんによる）

角BANの大きさによらず、CP＝ＡＢとなります。
（分かり易くするため下図では、ＡＢ＝５ｃｍ、ＢＰ＝３ｃｍ、ＡＰ＝４ｃｍにしています。
　ＡＢを一定にしてＡ，Ｂを動かしたとき、ＣはＰを中心とする半径５ｃｍの円周上を動きます。）

参考図４