第１５８問の解答

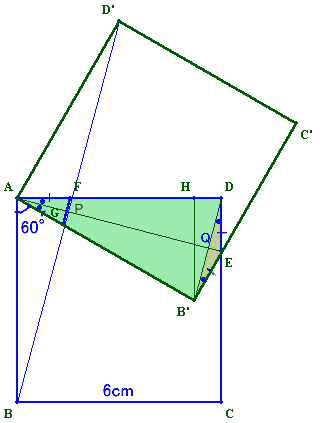
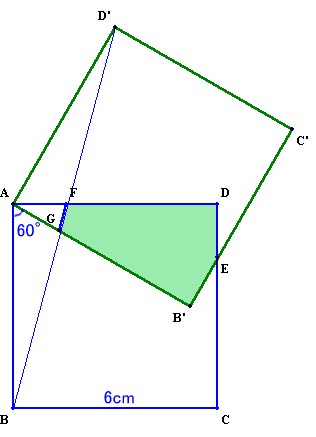
１．問題　［平面図形］

問題図
左図は、一辺の長さが６cmの正方形ＡＢＣＤを、頂点Ａを中心に６０゜回転させたところです。

　このとき、図中の五角形ＦＧＢ’ＥＤの面積を求めてください。

２．解答例１(長野美光さん、H.Takaiさん、RYO-chinさん、ｋｕｒｉ他)

ＡＥとＦＧの交点をＰ、Ｂ'Ｄとの交点をＱとします。

参考図１

ＡＢ＝ＤＡ、∠ＡＢＦ＝∠ＤＡＥ＝１５°、∠ＢＡＦ＝∠ＡＤＥ＝∠Ｒより、△ＡＢＦと△ＤＡＥは合同な直角三角形となります。
よって、ＡＦ＝ＤＥ。

従って、△ＡＰＦ、△ＡＰＧ、△ＤＱＥ、△ＤＢ'Ｅは全て合同な直角三角形、
よって、△ＡＦＧの面積＝△ＤＢ'Ｅの面積となります。

これより、五角形ＦＧＢ'ＥＤの面積
　　＝△ＡＢ'Ｄの面積
　　＝1/2×ＡＤ×Ｂ'Ｈ＝1/2×６×３＝９ｃｍ2
となります。

答：９ｃｍ2

以上

３．解答例２(わかさひ君、おりくん他)

五角形ＦＧＢ'ＥＤの面積＝△ＡＢ'Ｄの面積、までは解答例１と同じ。

△ＡＱＤ、△ＡＱＢ'、△Ｄ'ＡＰ、△ＢＡＰは全て合同な直角三角形。
よって、△ＡＢ'Ｄの面積＝△ＡＢＤ'の面積
　　　＝1/2×ＡＢ×（Ｄ'からＡＢの高さ）
　　　＝1/2×６×３＝９ｃｍ2

以上