第１６０問の解答

１．問題　［平面図形］

問題図

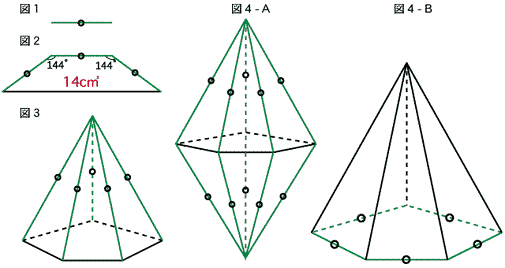
　上の図１のような竹ひごを使って、図２のような台形を作ったところ、面積が１４cm2となりました。
　　竹ひご５本を使って図３のような正５角すいを作りました。このとき、側面の二等辺三角形の頂角は３６゜でした。

（１）この正５角すいの表面積を求めてください。

（２）図４−Ａは、図３の正５角すいを２つ組み合わせて作った１０面体です。
　　　図４−Ｂは、底面の部分に竹ひごを使って図３の正５角すいと相似な立体を作ったものです。

　　　このとき、図４−Ａの立体と、図４−Ｂの立体の表面積の合計を求めてください。

２．解答例１(YokoyaMacさん、マサルさん、ありさのお父さん、丸天後藤様他)

（設問１）

図３の正５角錐の展開図は下記の図５のような星形で表せることが出来ます。
台形の面積をＳ０、星形の面積をＳ１とします。

参考図０

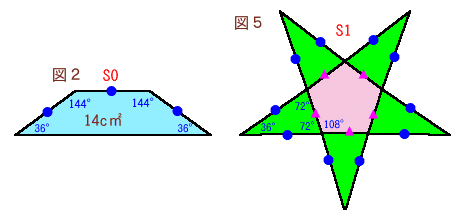
図２、図５を下記のように分割します。

参考図１

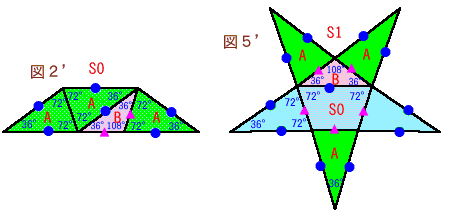
図２’より、台形は頂角３６度の２等辺三角形Ａ×３個と頂角１０８度の２等辺三角形Ｂ×１個に分割されます。

一方、図５’より正５角錐の展開図は、台形１個とＡ×３個、Ｂ×１個に分割されていますので、面積Ｓ１＝Ｓ０×２＝２８ｃｍ2となります。

（設問２）

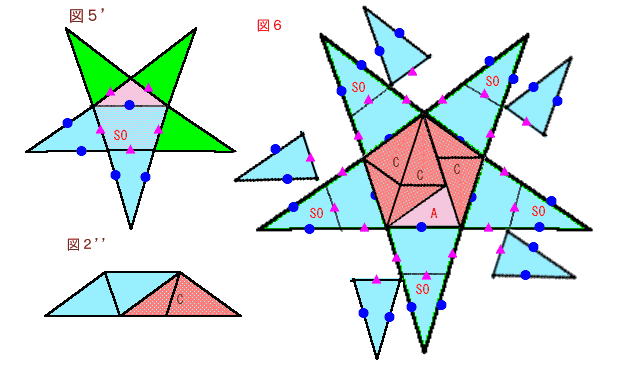
図５’より、大きい正５角錐の側面１個と元の正５角錐の側面１個（Ａ）でちょうどＳ０と等しくなります。

参考図２

従って、側面５個ずつでは、Ｓ０×５となります。

次に、図６の正５角形は、図２''のＣが３個とＡが１個に分割されます。
これにＡを５個加えると、Ｃが３個とＡが６個＝Ｓ０×３となります。

従って、求める面積＝Ｓ０×８＝１１２ｃｍ2となります。

答：(1)２８ｃｍ2
　　　(2)１１２ｃｍ2

以上