第１６１問の解答

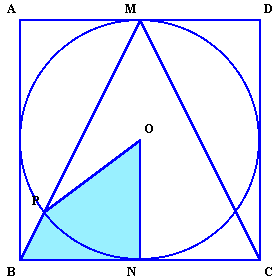
１．問題　［平面図形］

問題図
　左図で、四角形ＡＢＣＤは、一辺の長さが６cmの正方形です。

　この正方形の内部に、正方形の４つの辺すべてと接する円をつくり、その中心をＯとします。

　また、ＡＤ、ＢＣの中点をＭ、Ｎとし、ＭＢと円の交点をＰとします。

　このとき、四角形ＢＰＯＮの面積を求めてください。

２．解答例１(長野美光さん、YokoyaMacさん他)

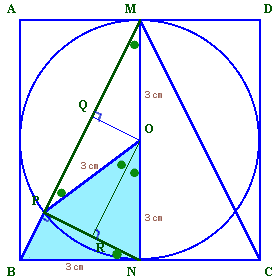
ＰからＢＮ、ＭＮに下ろした垂線の足をＱ、Ｒとします。

参考図

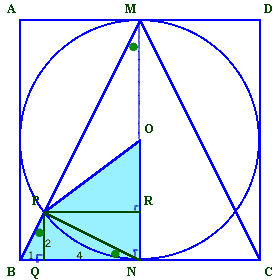
△ＭＢＮ、△ＰＢＱ、△ＮＰＱは相似な直角三角形で、直角を挟む２辺の比は１：２。

従って、ＢＰ：ＰＱ：ＱＮ＝１：２：４となります。
ＢＮ＝ＢＣ／２＝３ｃｍだから、ＢＰ＝３／５ｃｍ、ＰＱ＝６／５ｃｍ、ＱＮ＝１２／５ｃｍとわかります。

従って、求める面積
　　　＝△ＮＢＰ＋△ＯＰＮ
　　　＝1/2×３×６／５＋1/2×３×１２／５
　　　＝２７／５ｃｍ2となります。

答：２７／５ｃｍ2

以上

２．解答例２(わかさひ君、ありさのお父さん、アクトのよしおさん、H.Takaiさん、中村明海さん他)

∠ＭＰＮは直径ＭＮに対する円周角だから直角となります。

円の中心ＯからＭＢ、ＮＰに下ろした垂線の足をＱ、Ｒとします。

参考図１

△ＮＢＰと△ＭＯＱは、ＮＢ＝ＭＯ＝３ｃｍ、∠ＢＮＰ＝∠ＯＭＱ、∠ＢＰＮ＝∠ＯＱＭ＝９０°なので合同。

△ＯＭＰは２等辺三角形なので、△ＭＯＱと△ＯＰＱは合同。

同様に△ＯＰＲと△ＯＮＲは合同。

また四角形ＯＱＰＲは直角形なので、△ＯＰＲと△ＯＰＱは合同。

以上から、△ＭＢＮは５つの合同な三角形に分割され、四角形ＢＰＯＮはそのうち３個よりなる。

よって、四角形ＢＰＯＮ＝3/5×（1/2×３×６）＝２７／５ｃｍ2となります。