第１６２問の解答

---

１．問題　［空間図形］

左図で、底面が正三角形であるエンピツがあります。このエンピツのいろいろな部分の長さを測ってみました。 　その結果、ＯＡ＝１０mm、ＭＨ＝３mmでした。ただし、Ｍは曲線ＡＢの 中点、Ｈは線分ＡＢの中点です。 　このとき、次の各問いに答えてください。 (1)このエンピツを、Ｍを通り底面に平行な面で切断しました。 このとき、Ｏが含まれている方（円すいですね）の体積を求めてください。 (2)ＣＨの長さを求めてください。

---

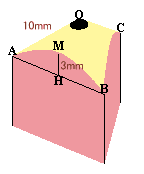２．解答例１(ありさのお父さん、YokoyaMacさん、長野美光さん、CRYING DOLPHINさん他)

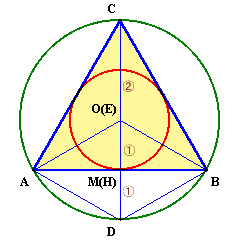
エンピツを上から見たところを図１、右から見たところを図２とします。

図１（平面図）

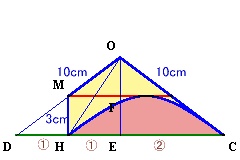
図２（側面図）

図１で頂点Ｏから底面に下ろした垂線の足をＥとすると、Ｅは正三角形ＡＢＣの重心となります。
ＣＨの延長線とＡＢＣの外接円との交点をＤとすると、ＣＥ：ＥＨ：ＨＤ＝２：１：１。

図２で頂点ＯからＭを通り底面に平行な面に下ろした垂線の足をＦとします。

直角三角形ＯＤＥについてＭＨとＯＥは平行でＤＨ：ＨＥ＝１：１となるので、
中点連結定理より、ＤＭ：ＭＯ＝１：１、ＭＨ：ＯＥ＝１：２となります。

従って、ＤＭ＝ＭＯ＝５ｃｍ、ＯＥ＝ＭＨ×２＝６ｍｍ、ＯＦ＝ＦＥ＝ＭＨ＝３ｍｍとなります。
よって、直角三角形ＭＤＨは斜辺が５ｍｍ、１辺が３ｍｍですから、もう１辺のＤＨ＝４ｍｍとなります。

従って、円錐の体積＝1/3×４²×π＝16/3π＝５０．２４mm³となります。
また、ＣＨ＝ＨＥ＋ＥＣ＝１２ｍｍとなります。

答：（１）５０．２４mm³
（２）１２ｍｍ　

以上

---