第１６４問の解答

１．問題　［空間図形］

問題図
　左図のような「たこ型」と言われるＡＢ＝ＡＤ、ＢＣ＝ＤＣの四角形があります。また、∠ＡＢＣ＝∠ＡＤＣ＝９０°です。
z 　この四角形の、ＡＣとＤＢの交点をＰとすると、ＡＰ＝５０cm、ＰＣ＝８cmでした。
　さて、この四角形に３本の折り目をつけて折って、四面体を作ります。このとき、四面体は２種類つくることができます。

では、この２種類の四面体の体積比を求めてください。

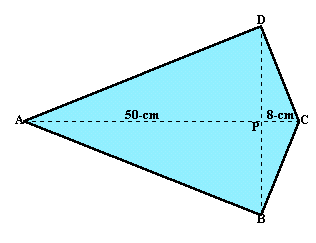２．解答例１（takashiさん、おりくん、yokoyaMacさん、T.Endoさん、貞松篤さん他多数）

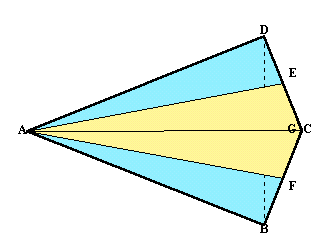
四角形ＡＢＣＤはＡＣを軸にして対象なので、四角錐となるような折り目の付け方は、

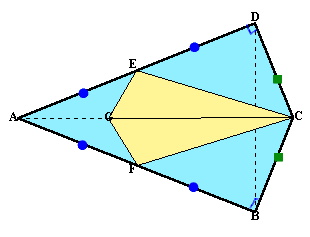
　図１：ADの中点をＥ、ABの中点をFとすると、折り目をＥＦ、ＥＣ、ＦＣとする
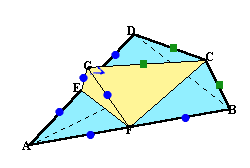
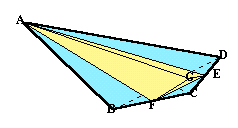
　図２：ＣDの中点をＥ、ＣBの中点をFとすると、折り目をＥＦ、ＥＡ、ＦＡとする

の２通りあります。

図１（平面図）
参考図１
 図１（俯瞰図）
参考図２
図２（平面図）
参考図３		 図２（俯瞰図）
参考図２

図１で∠ＣＧＥ＝∠ＣＧＦ＝９０°より、平面ＥＦＧと辺ＧＣは垂直に交わっている。
よって、四角錐の体積＝△ＥＦＧ×ＧＣ／３。

同様に、図２では四角錐の体積＝△Ｅ'Ｆ'Ｇ'×Ｇ'Ａ／３。

さて、△ＥＦＧ＝△ＥＦＡ＝△ADB×1/4=△ADP×1/2、
　　　△Ｅ'Ｆ'Ｇ'＝△ＥＦC＝△CDB×1/4=△ＣDP×1/2
△ＥＦＧ：△Ｅ'Ｆ'Ｇ'＝△ADP：△ＣDP＝ＡＰ：ＰＣ＝２５：４。

△ADPと△ＣDPは相似な直角三角形で相似比ｋはｋ＝ＡＰ：ＰＤ＝ＰＤ：ＰＣ、
ｋ2＝ＡＰ／ＰＤ×ＰＤ／ＰＣ＝ＡＰ／ＰＣ＝５０/８、ｋ＝√（５０/８）＝５/２。

よって、ＧC：Ｇ'A＝DC:DA=k=５/２。

四角錐の体積比＝（△ＥＦＧ：△Ｅ'Ｆ'Ｇ'）×（Ｇ'A：ＧC）=２５：４×２/５＝５/２。

答：５：２

以上