第１６５問の解答

１．問題　［平面図形］

問題図
　左図のに、四角形ＡＢＣＤの頂点Ａと頂点Ｃ、頂点Ｂと頂点Ｄを結び、それぞれの中点Ｎ、Ｍを取りました。また、ＡＣとＢＤの交点をＰとします。

　四角形ＡＢＣＤの面積は８０cm2、三角形ＡＭＣの面積は２０cm2、三角形ＢＮＤの面積は１２cm2となっています。

　このとき、三角形ＰＢＣの面積を求めてください。

２．解答例１（長野　美光さん、えくさーつー(爆)(阿)さん、ありさのお父さん他多数）

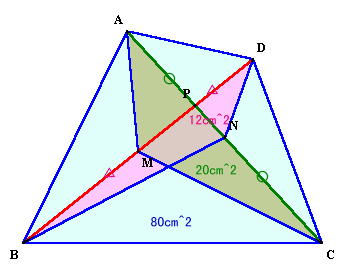
ＡＮ＝ＮＣより、△ＡＢＮ＝△ＣＢＮ、△ＡＤＮ＝△ＣＤＮ。
よって、四角形ＡＢＮＤ＝四角形ＣＢＮＤ＝四角形ＡＢＣＤ／２＝４０ｃｍ2。
同様に、四角形ＡＢＣＭ＝四角形ＡＭＣＤ＝四角形ＡＢＣＤ／２＝４０ｃｍ2。

よって、△ＢＣＤ＝四角形ＣＢＮＤ＋△ＢＮＤ＝４０＋１２＝５２ｃｍ2。

△ＡＣＤ＝四角形ＡＭＣＤ−△ＡＭＣ＝４０−２０＝２０ｃｍ2。
よって、ＭＰ＝ＰＢ。

従って、△ＰＢＣ＝△ＢＣＤ×3/4＝５２×3/4＝３９ｃｍ2。

答：３９ｃｍ2

以上

（参考）真ん中の四角形の面積を求める

次の２つの定理を使います。

［定理］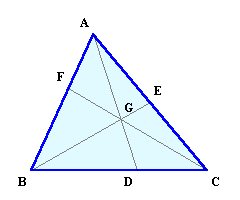
参考図１

Ｇは、三角形内
の任意の点



 
ＡＦ　ＢＤ　ＣＥ
━━・━━・━━＝１・・・チェバの定理
ＢＦ　ＣＤ　ＡＥ
 
ＡＦ　ＢＣ　ＤＧ
━━・━━・━━＝１・・・メネラウスの定理
ＢＦ　ＣＤ　ＡＧ
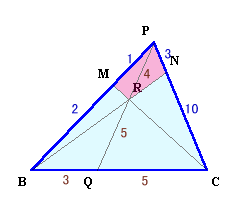
△ＰＢＣの部分
参考図２

チェバの定理より、
　　ＰＭ/ＭＢ×ＢＱ/ＱＣ×ＣＮ/ＮＰ＝１、
　　１/２×ＢＱ/ＱＣ×１０/３＝１、
よって、ＢＱ/ＱＣ＝３/５。

メネラウスの定理より、
　　ＰＭ/ＭＢ×ＢＣ/ＱＣ×ＱＲ/ＲＰ＝１、
　　１/２×８/５×ＱＲ/ＲＰ＝１、
よって、ＱＲ/ＲＰ＝５/４。

△ＰＲＭ＝△ＰＢＲ×1/3＝（△ＰＢＱ×４/９）×1/3＝（△ＰＢＣ×３/８）×４/９×1/3

△ＰＲＮ＝△ＰＣＲ×３/１３＝（△ＰＣＱ×４/９）×３/１３＝（△ＰＢＣ×５/８）×４/９×３/１３

よって、四角形ＰＭＲＮ
　　＝△ＰＲＭ＋△ＰＲＮ
　　＝△ＰＢＣ×１４/（３９×３）
　　＝１４／３ｃｍ2