第１６７問の解答

１．問題　［空間図形］

問題図
　　左図左のような、ＯＰ＝５cmの円すいがあります。

　この円すいに、左図右のようなＡＢ＝ＡＣ＝５cm、ＢＣ＝８cmの二等辺三角形の紙を巻きつけることにしました。円すいの母線であるＯＰとＡＢが重なるようにして巻きはじめたところ、二等辺三角形はこの円すいを２周しました。そして、点Ｃはちょうど点Ｐ（二等辺三角形でいえばＢ）と重なったそうです。

　では、この円すいの側面上で、二等辺三角形の紙が２重に巻かれている部分の面積は何cm2でしょうか。

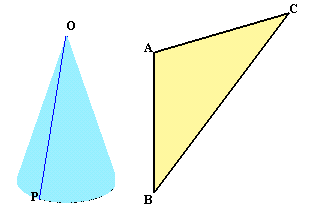２．解答例１（多数）

二等辺三角形（黄色）を巻き付けて２重になった部分をピンク色にすると、下図のようになります。展開図で考えましょう。

参考図１ 参考図２

円弧ＢＣの中点をＤ、辺ＢＣの中点をＦとします。
ＢＣ＝８cmだから、ＢＦ＝ＦＣ＝４cm、従って、△ＡＢＦ、△ＡＦＣは、辺の長さが３、４、５cmの直角三角形になります。
２周してＣがＢに重なるので、１周ではＤがＢに重なります。
２週目は右半分の扇形ＡＤＣをＡを中心に回転してＡＢＤに重ねればいいことになります。

従って、重なる部分は、直角三角形ＡＥＧとＡＧＦを合わせたものになります。
ＡＥ＝ＡＦ＝３cmより、ＥＢ＝５−３＝２cmとなり、△ＢＥＧは△ＢＦＡと相似だから、ＥＧ＝ＥＢ×３/４＝２×３/４＝３/２cmです。

よって、求める面積＝（１/２×３×３/２）×２＝９/２cm2となります。

答：９/２cm2

以上