第１６８問の解答

１．問題　［空間図形］

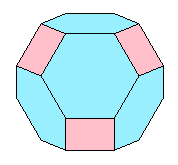
　面積が１８cm2である正方形が６枚と、正方形と一辺の長さが等しい正六角形が８枚あり、この１４枚を面とする多面体（１４面体ですね）をつくります。

　このとき、完成した多面体の体積を求めてください。

２．解答例１（CRYING DOLPHINさん、中村明海さん、HALさん他多数）

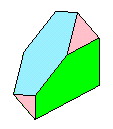
まず、問題の立体（動く３Ｄ図）がどのようになっているかを考えましょう。

図1
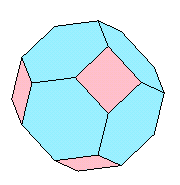
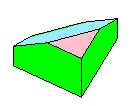
参考図1		 図2
参考図2		 図3
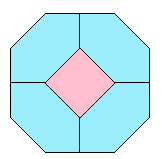
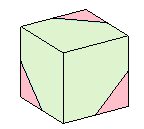
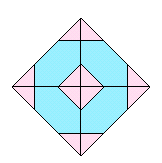
参考図3

図3を上から見た平面図とすると、立面図、側面図も同じ形になります。
これから、求める立体は立方体から8個の頂点を切り取った形と考えられます。

また、立方体の1辺の長さは、ちょうど元の正方形の対角線の2倍＝6×2＝12cmとなります。

さて、立方体を8等分すると図4、図5、図6のようになり、これを回転したものとを合わせると、図7のようにちょうど小さな立方体になります。

図4
参考図4		 図5
参考図5
図7
参考図6		 図8
参考図7

これより、求める立体の体積が大きな立方体の体積の半分
＝１２3/2＝８６４cm3であることが分かります。

答：８６４cm3

以上

３．解答例２（わかさひ君、sambaGREENさん、貞松篤さん他多数）

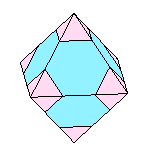
問題の立体の６つの正方形の上に正四角錐を乗せると正八面体（動く３Ｄ図）になります。

図7
参考図8		 図8
参考図9

まず、正八面体の体積を２つの正四角錐に分けて求めます。
正四角錐の底面は小さな正方形の３×３倍＝１８×９＝１６２cm2、
高さは９cmだから、体積＝1/3×１６２×９＝４８６cm3。

小さな四角錘は、大きな四角錘と相似で1/3の大きさだから体積は1/27。

よって、求める立体の体積＝四角錘×（２-1/27×６）＝４８６×16/9＝８６４cm3。