第１６９問の解答

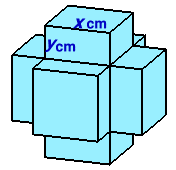
１．問題　［整数の性質］

問題図
　上の図のように、２種類（ｘcm、ｙcm）の竹ひごを使って立体を作りました。この立体は、前・後・右・左のどちらから見ても十字形に見えるそうです。この立体に紙で面を付けたところ、表面積が２８８cm2でした。

　では、この立体の体積は何cm3でしょうか。ただし、竹ひごの長さは２種類ともcmの単位で整数であるものとします。

２．解答例１（T.Endoさん、俊介さん、TORAさん、ヒデー王子さん他）

立体の表面積は、６（ｘ2＋４ｘｙ）＝２８８cm2なので、
　　ｘ（ｘ＋４ｙ）＝４８　・・・　（１）
となります。

これから、ｘは４８の約数（１，２，３，４，６，８，１２，１６，４８）で、ｘ＜ｘ＋４ｙより１≦ｘ≦６となります。

（１）より、ｙ＝（４８−ｘ2）／４ｘとなりますので、１≦ｘ≦６でｙの値が整数となるものは下表からｘ＝４、ｙ＝２のみとなります。

参考図1

これより、求める立体の体積＝ｘ3＋６ｘ2ｙ＝４3＋６×４2×２＝４４＝２５６cm3となります。

答：２５６cm3

以上

３．解答例２（マサルさん、航介さん他）

（１）式より、ｘ、ｘ＋４ｙは４８の約数のうち、掛けて４８、差が４の倍数となるものを求めることになる。

参考図2

４８＝４×１２の１組のみで、ｘ＝４、ｘ＋４ｙ＝１２よりｘ＝４、ｙ＝２となる。
以下同様。

４．解答例３（大西俊郎さん、航介さん、ｋｕｒｉ他）

（補題）ｎが整数のとき、ｎ2が偶数なら、ｎも偶数
なぜなら、もしｎが奇数とすると、ｎ2も奇数となり矛盾。


（１）より、ｘ2＝４８−４ｘｙとなり、ｘ2が偶数なので、ｘも偶数、ｘ＝２ｐと書ける。

４ｐ2＝４８−８ｐｙ、ｐ2＝１２−２ｐｙ、よってｐ2が偶数なので、ｐも偶数、ｐ＝２ｑと書ける。

４ｑ2＝１２−４ｑｙ、ｑ2＝３−ｑｙ。
０＜ｑ2＜３より、ｑ＝１、ｙ＝３−１＝２、ｘ＝４ｑ＝４となる。