第１７０問の解答

---

１．問題　［場合の数？］

あるクラスで、カードを使ったゲームをしました。 　まず、クラス人数の２倍の枚数のカードを用意し、１から順に通し番号を記入しました。次に、生徒たちに２枚ずつカードを配ります。 　生徒は、受け取った２枚のカードの番号の差を自分の得点とします。例えば、１４番と２３番のカードを受け取ったなら、得点は２３−１４＝９点となります。  　このとき、全員の得点の和は、最も大きいときで４００点になります。 　では、全員の得点の和は、全部で何通り考えられるでしょうか。

---

２．解答例１（TORAさん、CRYING DOLPHINさん、Miki Sugimotoさん、俊介さん他）

クラスの人数をｎ人とします。

まず、次のことを示します。

得点の和の最小値はｎ、最大値はｎ2 得点の和は、全て２で割った余りが等しい 　　（初期値ｎ、公差２の数列）

（最小値）
クラスの生徒に１連番号を振ります。
ｍ番目の生徒が受け取るカードを［a_m,b_m］(a_m<b_m)とすると、1≦b_m-a_mより、
得点の和S=Σ(b_m-a_m)≧ｎとなります。
実際、[1,2],[3,4],・・・[2n-1,2n]のときS=nとなるので、Sの最小値＝nとなります。

（最大値）
S=Σb_m-Σa_m
　≦{(n+1)+(n+2)+・・+2n}-{1+2+・・+n}
　={1+2+・・+2n}-{1+2+・・+n}×2
　=2n×(2n+1)/2-n×(n+1)/2×2
　=n×(2n+1)-n×(n+1)
　=n²
実際、[1,n+1],[2,n+2],・・・[n,2n]のときS=n²となるので、Sの最小値＝n²となります。

(２で割った余りが等しい)
S=(Σb_m+Σa_m)-２×Σa_mより、SとSS＝(Σb_m+Σa_m)＝n×(2n+1)の差は偶数。
よってSSが偶数（n：偶数)ならSは常に偶数、SSが奇数（n：奇数)ならSは常に奇数。

以上から、最大値n²＝400よりn=20。
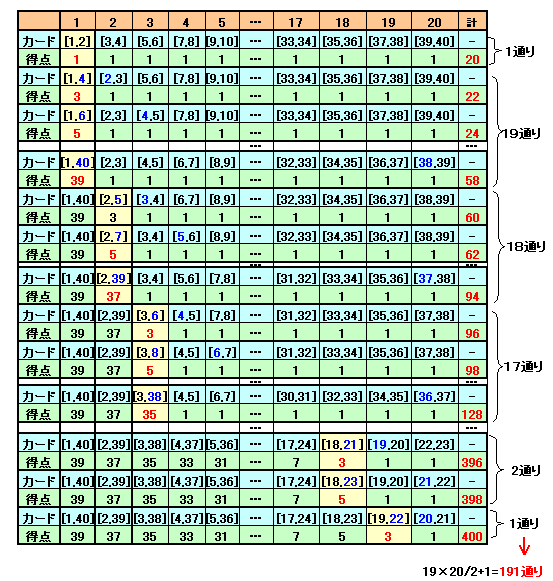
また、Ｓがとる値の場合の数は、(n²-n)/2+1=(400-20)/2+1=191。

答：１９１

（補足）
厳密にいうと、Ｓはnからn²までの任意の偶数または奇数の値をとることを示す必要がある。下記は、n=20のときの１例である。

以上

---

（帰納法による補足の証明）

n=kのときに補足が成り立つ（Sは、kからk²+1のk(k-1)/2+1通りの偶数または奇数の値をとる）と仮定する。

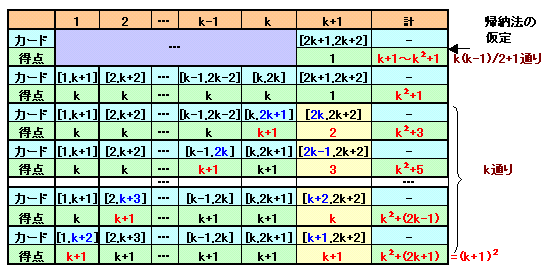
n=k+1のとき：
k+1番目の生徒のカードを[2k+1,2k+2]（得点１）とすると、帰納法の仮定からk番目の生徒までの得点がk〜k²なので、合計k+1〜k²+1。

さらに上図のように、k+1番目の生徒の小さいカードとk番目〜１番目の生徒の大きいカードとを次々と交換していけば、得点は２点ずつ増えて最大(k+1)²になる。

よって、n=k+1のときにも補足は成り立つ。

以上から、数学的帰納法により、任意のnについて補足が成り立つことが示された。

---