第１７１問の解答

---

１．問題　［平面図形］

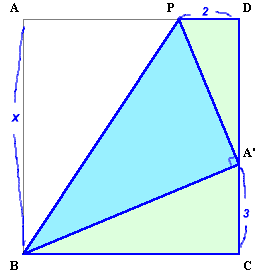
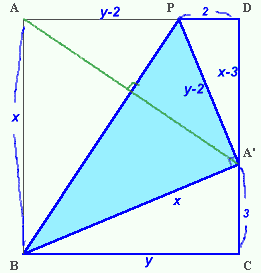
上の図は、長方形ＡＢＣＤの頂点Ａが、辺ＤＣ上にくるようにＰＢを折り目として折ったところを示しています。 　では、ＣＡ’＝３cm、ＤＰ＝２cmのとき、ＡＢの長さは何cmでしょうか。

---

２．解答例１（ありさのお父さん、丸天後藤様、ＴＯＲＡさん他）

ＡＢ＝ｘ、ＡＤ＝ｙとおく。

題意より、△ＡＰＢと△Ａ’ＰＢはＰＢを軸として対称である。
ＰＡ’＝ＰＡ＝ｙ−２、Ａ’Ｂ＝ＡＢ＝ｘで、△Ａ’ＰＤ、△Ａ’ＢＣは共に直角三角形だから、
　　（ｘ−３）²＋２²＝（ｙ−２）²　・・・（１）
　　ｘ²＝ｙ²＋３²　・・・（２）

（１）−（２）より、
　　−６ｘ＋９＋４＝−４ｙ＋４−９、よってｙ＝（ｘ−３）×3/2

（２）に代入して、
　　ｘ²＝（ｘ−３）²×9/4＋３²
　　５ｘ²−５４ｘ＋１１７＝０
よって、（５ｘ−３９）（ｘ−３）＝０
ｘ＞３だからｘ＝３９／５＝７．８ｃｍとなります。

答：7.8cm

　以上

---

３．解答例２（長野　美光さん、中村明海さん、まるケンさん、Hamayanさん他）

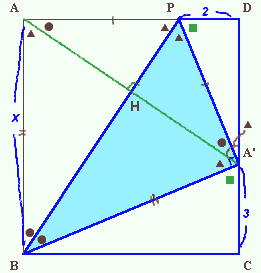
まず、△ＡＰＢと△Ａ’ＰＢはＰＢを軸として対称であることから、
∠BAA'＝∠BA'A、∠ABP＝∠A'BP、∠PAA'＝∠PA'A、∠APB＝∠A'PBとなります。
また、∠BAA'＋∠PAA'＝９０°などから、結局、
　∠BAA'＝∠BA'A＝∠APB＝∠A'PB＝▲
　∠ABP＝∠A'BP＝∠PAA'＝∠PA'A＝●　と分かります。

従って、∠DA'A＝９０°−●＝▲となり、
∠DPA'＝∠CA'B＝９０°−２×▲＝■と分かります。

よって、△DPA'と△CA'Bは相似で、相似比はDP：CA'＝２：３となります。
従って、PA'：A'B＝２：３なので、AP＝PA'＝２ｔ、AB＝A'B＝３ｔ　と書けます。

また、A'D＝ＡＢ−A'C＝３ｔ−３、AD＝AP＋ＰＤ＝２ｔ＋２で、
A'D：PD＝BC：A'Cより、（３ｔ−３）：２＝（２ｔ＋２）：３、
これをｔに関して解くと、ｔ＝２．６、よってAB＝A'B＝３ｔ＝７．８ｃｍと分かります。　

---

４．解答例２（ヒデー王子さん）

解答例２と同様にして、△PA'Dと△A'BCが相似で相似比は２：３。
また、△PAH：△BAH＝△PA'H：△BA'H＝２：３なので、各面積比は４：９。
△AA'Dの面積：四辺形ABCA'＝４：９。

△A'BC＝（四辺形ABCA'−△AA'D）／２だから△AA'D：△A'BC＝４：２．５、
DA'：A'C＝△AA'D：△A'BC＝４：２．５。

よって、AB＝CD＝A'C×（４＋２．５）／２．５
　　　　　　　＝３×６．５／２．５＝３９／５＝７．８ｃｍ。

---