第172問の解答
1.問題 [速さ]
| あるデパートの2Fから3Fに向かう上りエスカレーターで、マサルさんとトモエさんが遊んでいました。 あるとき、トモエさんが2Fから3Fへ、マサルさんが3Fから2Fへ同時に歩き始めました。トモエさんは3Fに着くとすぐに2Fに向かって、マサルさんは2Fに着くとすぐに3Fに向かって歩き始めます。このとき、マサルさんが1度目にトモエさんに出会ってから2度目に出会うまでに下り方向には60歩、上り方向には15歩だけ歩いたそうです。 さて、今度はマサルさんが3Fから2Fに向かって歩き、トモエさんは2Fから買い物カゴをエスカレーターに乗せて(置いて)3Fに向かわせる遊びをしました。このとき、 (1) マサルさんは2Fから数えて何段目の地点で買い物カゴと出会ったでしょうか。 (2) マサルさんは買い物カゴを受け取るまでに何歩歩いたでしょうか。 ただし、2人の歩くペースは同じものとします。 |
2.解答例1
マサルさん、トモエさんがエスカレータを下る時の速さと上るときの速さの比を1:kとする。
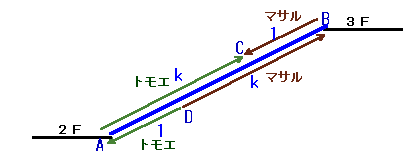
2人が出発して1回目に出会うまでに進む段数の比はBC:AC=1:k、2回目に出会ってもとの階に戻るときの段数の比はBD:AD=k:1となる。
マサルさんが、AC間を下りるときとAD間を上るときの速度比が1:kで、段数の比がk:1だから所用時間の比はk2:1=60:15=4:1。よって、k=2となります。
これから、エスカレータ自身が上がる速さをv0、2人が進む速さをv1とすると、(v1+v0):(v1-v0)=2:1、よってv1:v0=3:1と分かります。
さて、マサルさんは、AC間を3×v0の速度で60歩下りましたが、その間エスカレータがv0の速度で上がったため、正味に下りた段数は60×2/3=40段、BC間の段数は40段×1/2=20段になります。
(同様に、AD間の段数=15×4/3=20段、BD間の段数=20×2=40段となります。)
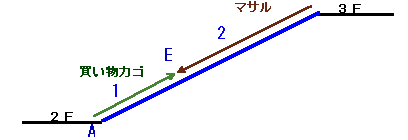
さて、次のゲームで買い物カゴの上がる速度はv0、マサルさんの下りる速度は2×v0で速度比は1:2。よって、出会うまでに進む段数の比は1:2、よってAE=60×1/3=20段。
この間に、マサルさんは3倍の速度で進んだので、20×3=60歩となります。
答:(1)20段(2)60歩
参考図
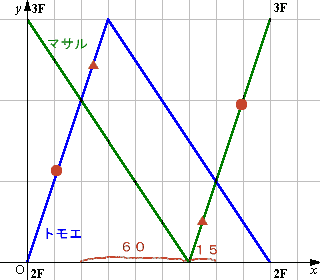
以上