第１７３問の解答

---

１．問題　［平面図形］

左図のように、板の上に１.５cmの間隔でクギを２本打ちつけました。この２本のクギに直径３cmの輪がかけてあります。 　この輪を板から離さないで動かすとき、輪（円周）が通ることのできる部分の面積は何cm2でしょうか。円周率を３.１４として答えてください。

---

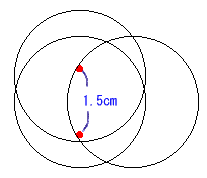２．解答例１（長野　美光さん他）

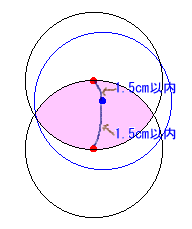
輪の中心と２本のクギとの距離は、輪の半径である１．５ｃｍ以内でなければならないので、輪の中心がクギのところにある２つの円の交わる部分内（図１）を動くこととなる。
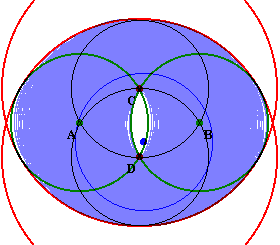
実際に動かした軌跡が図２である。

図１

図２

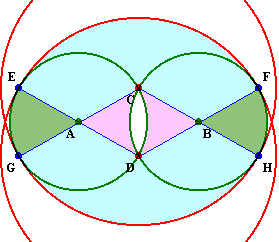
図２を見ると、図３のように、輪が２本のクギＢ、Ｃをちょうど通るときの円Ａ、円Ｂ、および中心がＣ、Ｄで半径が３ｃｍの円Ｃ、円Ｄで区分されるいくつかの部分からなっていることが分かります。

図３

　求める面積
＝扇形ＡＧＥ＋扇形ＢＦＨ＋（扇形ＤＥＦ＋扇形ＣＧＨ−菱形ＡＤＢＣ）−レンズＣＤ
＝扇形ＤＥＦ＋扇形ＣＧＨ＋（扇形ＡＧＥ＋扇形ＢＦＨ）−（菱形ＡＤＢＣ＋レンズＣＤ）
＝扇形ＤＥＦ＋扇形ＣＧＨ
＝（π×３²×1/3）×２
＝３．１４×６
＝１８．８４ｃｍ²

答：18.84cm²

　以上

---