第１７８問の解答

１．問題　［平面図形］

問題図
　左図のように、角ＸＯＹ＝４５゜となっている２直線ＯＸ、ＯＹがあります。

　いま、ＯＡ＝４cmとなる点ＡをＸＯＹの内部にとり、
ＯＸ上に点Ｂを、ＯＹ上に点Ｃを三角形ＡＢＣの周の長さが最も短くなるようにとりました。

　このとき、ＢＣとＯＡの交点をＰとすると、ＯＰ＝３cm、ＰＡ＝１cmであったそうです。

　では、三角形ＡＢＣの面積は何cm2と考えられるでしょうか。

２．解答例１（YokoyaMacさん、わかさひ君、ヒデー王子さん、Hamayanさん、中村明海さん他多数）

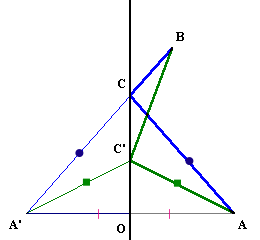
（参考問題）点Ａ，Ｂがある直線に対して同じ側にあります。
　　　　　　　直線上の点Ｃが動くとき、ＡＣ＋ＢＣが最小になる点Ｃの位置は？

参考図1 （解答例）
直線に対して、Ａと対称な点をＡ’とする。
点ＣをＡ'Ｂと直線の交点、C'はそれ以外の点とすると、
ＡＣ＝Ａ'Ｃ、ＡＣ'＝Ａ'Ｃ'、となることから、
　AC+BC=A'C+BC<A'C'+BC'=AC'+BC'

よって、点Ａ'、Ｃ、Ｂが一直線上にならぶときに、ＡＣ＋ＢＣが最小となる。

（本問の場合）

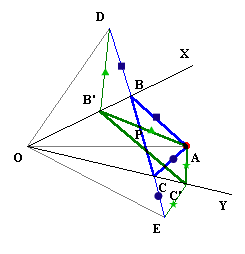
参考図2 直線ＯＸに関して点Ａと対称な点をＤ、直線ＯＹに関して点Ａと対称な点をＥとする。

ＡＢ＝ＢＤ、ＡＣ＝ＥＣより、
　ＡＢ＋ＢＣ＋ＣＡ＝ＤＢ＋ＢＣ＋ＣＥ

よって、Ｄ、Ｂ、Ｅが一直線上に並ぶとき、すなわちＢがＯＸとＤＥの交点、ＣがＯＹとＤＥの交点になるときに三角形ＡＢＣの周の和は最小となる。

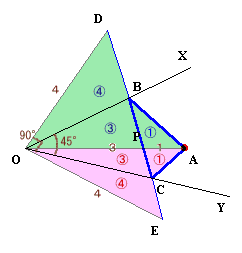
このとき、三角形ＡＢＣの面積は次のようにして求めることが出来ます。

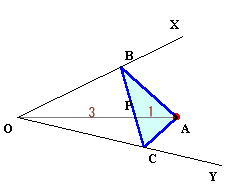
参考図3 ＯＰ：ＰＡ＝３：１より、
△ＯＢＰ：△ＡＢＰ＝△ＯＣＰ：△ＡＣＰ＝３：１。

また対称性より、
△ＯＤＢ＝△ＯＡＢ、△ＯＥＣ＝△ＯＡＣ。
よって、
△ＯＤＰ：△ＡＢＰ＝△ＯＥＰ：△ＡＣＰ＝７：１。
△ＤＯＥ：△ＡＢＣ＝７：１。

また、∠ＤＯＥ＝∠ＡＯＢ×２＋∠ＡＯＣ×２
　＝（∠ＡＯＢ＋∠ＡＯＣ）×２
　＝９０°。

従って、△ＤＯＥ＝1/2×ＤＯ×ＥＯ
　＝1/2×４×４＝８ｃｍ2。

よって、△ＡＢＣ＝1/7×△ＤＯＥ＝8/7ｃｍ2。

答：8/7ｃｍ2

　以上